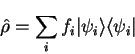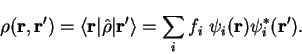Next: 4.4 Constraints on the
Up: 4. Density-Matrix Formulation
Previous: 4.2 Partial occupation of
Contents
We consider a system with a set of orthonormalised orbitals
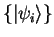 and occupation numbers
and occupation numbers 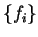 . The single-particle density-operator
. The single-particle density-operator 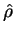 is defined by
is defined by
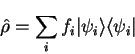 |
(4.21) |
and the density-matrix in the coordinate representation is
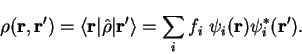 |
(4.22) |
The diagonal elements of the density-matrix are thus related to the electronic
density by
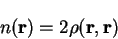 |
(4.23) |
and the generalised non-interacting kinetic energy is
![\begin{displaymath}
T_{\mathrm s}^{\mathrm J}[n] = 2 \int {\mathrm d}{\bf r'} \l...
..._{\bf r}^2 \rho({\bf r},{\bf r'})
\right]_{{\bf r}={\bf r'}} .
\end{displaymath}](img427.gif) |
(4.24) |
This expression can be written as a trace of the density-matrix and the
matrix elements of the kinetic energy operator
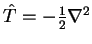 i.e.
i.e.
![$T_{\mathrm s}^{\mathrm J}[n] = 2 {\rm Tr} (\rho T)$](img429.gif) . Similarly, for the
energy of interaction of the electrons with the external (pseudo-) potential
. Similarly, for the
energy of interaction of the electrons with the external (pseudo-) potential
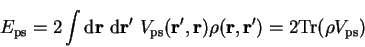 |
(4.25) |
where
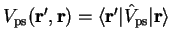 . The definitions of the Hartree
and exchange-correlation energies in terms of the electronic density
(now defined in terms of the density-matrix by equation 4.23)
remain unchanged. Thus we can express the total energy of both
interacting and non-interacting systems in terms of the density-matrix.
By minimising the energy with respect to the density-matrix (subject to
appropriate constraints to be discussed) we can thus find the ground-state
properties of the system.
. The definitions of the Hartree
and exchange-correlation energies in terms of the electronic density
(now defined in terms of the density-matrix by equation 4.23)
remain unchanged. Thus we can express the total energy of both
interacting and non-interacting systems in terms of the density-matrix.
By minimising the energy with respect to the density-matrix (subject to
appropriate constraints to be discussed) we can thus find the ground-state
properties of the system.




Next: 4.4 Constraints on the
Up: 4. Density-Matrix Formulation
Previous: 4.2 Partial occupation of
Contents
Peter Haynes
![]() and occupation numbers
and occupation numbers ![]() . The single-particle density-operator
. The single-particle density-operator ![]() is defined by
is defined by