Density-functional calculations

The Kohn-Sham (KS) equation for an $M$-electron system is[20,21]

$$\hat{H} \psi_m({\bf r}) = \left[-\frac{\hbar^2}{2m_{\mathrm{... ...f r}) \right] \psi_m({\bf r}) = \varepsilon_m \psi_m({\bf r}),$$ (6)

where $\{ \psi_m({\bf r}) \}$ are the KS eigenfunctions with corresponding eigenvalues $\{ \varepsilon_m \}$. The effective potential $V_{\mathrm{eff}}({\bf r})$ consists of the classical electrostatic potential, the ionic potential due to the nuclei and the exchange-correlation potential. The effective potential depends on the electron density, $\rho({\bf r})$, which is formed from the $M$ lowest eigenstates

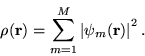$$\rho({\bf r}) = \sum_{m=1}^{M} \left\vert \psi_m({\bf r}) \right\vert^2.$$ (7)

We use the real spherical-wave basis set $\{\chi_{\nu}({\bf r})\}$ to expand the $n$-th KS eigenstate

$$\psi_n({\bf r}) = \sum_{\nu} {x_n}^{\nu} \ \chi_{\nu}({\bf r}),$$ (8)

where $\nu$ is a collective label for $(\alpha, n \ell m)$ in Eq. (5). Substituting Eq. (10) into Eq. (8), and taking inner products with the $\{ \chi_{\mu}({\bf r}) \}$, we obtain the generalized eigenvalue problem

$$\sum_{\nu} (H_{\mu \nu} - \varepsilon_n S_{\mu \nu}) {x_n}^{\nu} = 0,$$ (9)

where the overlap matrix is given by

$$S_{\mu \nu} = \int d{\bf r}\ \chi_{\mu}({\bf r}) \chi_{\nu}({\bf r}),$$ (10)

and the Hamiltonian matrix is given by

$$H_{\mu\nu} = \int d{\bf r}\ \chi_{\mu}({\bf r}) \hat{H} \chi_{\nu}({\bf r}).$$ (11)

It should be emphasized that when a large system is studied, $S$ and $H$ will be sparse. In this case it is more efficient to use an iterative method based on preconditioned conjugate gradient minimization[22] to find the lowest few eigenvalues and corresponding eigenvectors of Eq. (11) than to use a direct matrix diagonalization method [23,24] in which all eigenvalue-eigenvector pairs are found.

The completeness of the basis set depends on several parameters such as the radius of the basis sphere, $R$; the maximum angular momentum component, $\ell_{\mathrm{max}}$; and the number of $q_{n \ell}$ values for each angular momentum component, which we will take here to be the same for all $\ell$ and is denoted by $n_q$. The number of basis functions in a basis sphere is $(\ell_{\mathrm{max}}+1)^2 n_q$. For a fixed number of $n_q$, we note that the number of basis functions increases very rapidly with respect to $\ell_{\mathrm{max}}$. However, we will demonstrate that most physical properties can be deduced using only a small $\ell_{\mathrm{max}}$, which is typically 2. The cutoff energy $E_{\mathrm{c}}$ for a basis sphere is roughly given by

$$E_{\mathrm{c}} = \frac{\hbar^2}{2m_{\mathrm{e}}} \left( \frac{n_q \pi}{R} \right)^2.$$ (12)

Periodicity of the system under study is assumed and the $\Gamma$ point only is used for the Brillouin zone sampling. We have used the local density approximation (LDA) for the exchange and correlation term. Norm-conserving Troullier-Martins[25] pseudopotentials in the Kleinman-Bylander[19] form are used.