Results of the calculations

In this section we present and discuss the results obtained from density-functional calculations using the spherical-wave basis set. We study the convergence of the total energy as a function of the cutoff energy, $E_{\mathrm{c}}$ ; the radii of the basis spheres,

; the maximum angular momentum component, $\ell_{\mathrm{max}}$ ; and the number of basis spheres, $N_{\scriptstyle\mathrm{bs}}$ . Physical properties are deduced from total energy calculations on the systems. For molecules, we calculate the equilibrium bond lengths and force constants. For bulk crystalline silicon, we calculate the equilibrium lattice parameter and bulk modulus. These results are compared with those obtained using a plane-wave code[18], and from experiment[26].

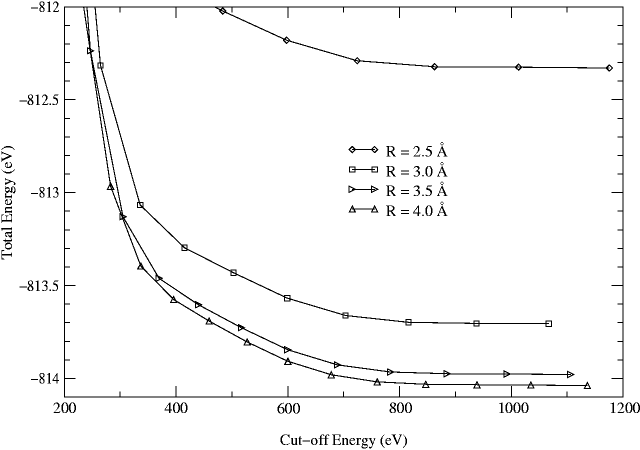
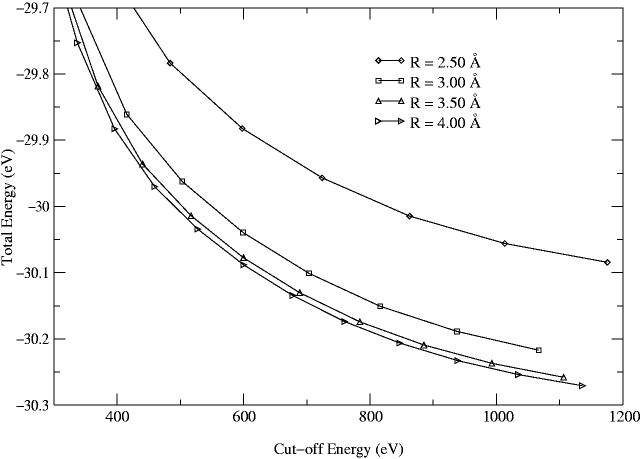
In Fig. 1 we plot the total energy of the chlorine molecule with a bond length of 1.6 Å as a function of cutoff energy $E_{\mathrm{c}}$ and basis sphere radius

. The figure shows that the total energy decreases rapidly as the cutoff energy and the basis sphere radius are increased, which is to be expected from the additional variational freedom that is introduced. Convergence in the total energy is achieved for cutoff energies above 800 eV.

**Figure 2:** Nature of the convergence of the total energy of the chlorine molecule with a bond length of 1.6 Å. The data for the spherical-wave basis set are taken from Fig. 1. The respective converged total energies are subtracted from the total energy in each case.

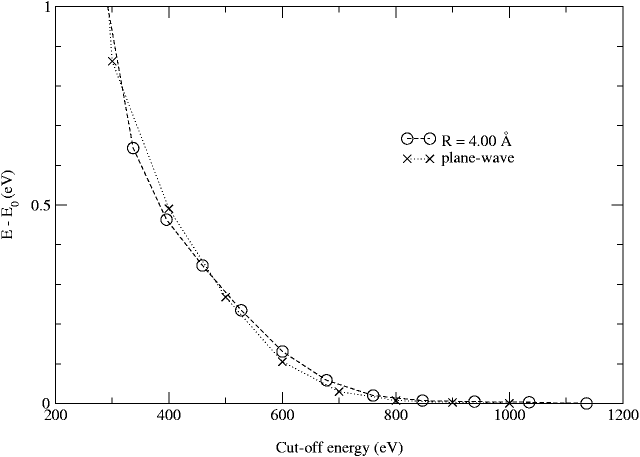
Fig. 2 shows that the rate of convergence of the total energy with respect to the cutoff energy is the same for both the localized spherical-wave and extended plane-wave basis sets. This confirms that the energy cutoff concept can be equally applied in the spherical-wave basis set.

**Figure 3:** Convergence of the total energy of the chlorine molecule for a variety of bond lengths. The respective converged total energies are subtracted from the total energy in each case. Two basis spheres of radius centered on the atoms are used. The dotted curves are exponential fits to the data.

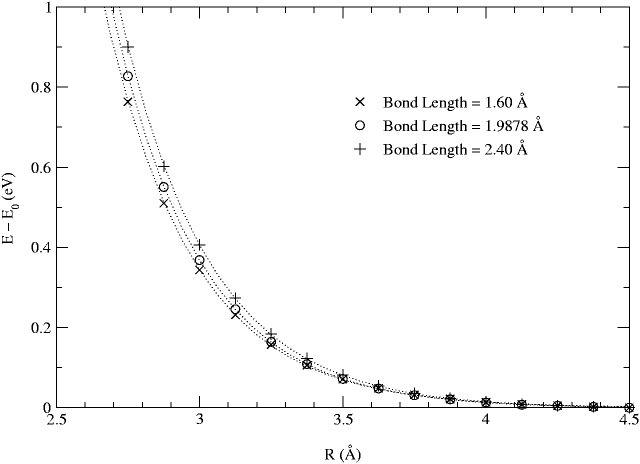
Using an energy cutoff above 900 eV, we calculate the total energy of the chlorine molecule for a variety of bond lengths as a function of the basis sphere radius

. Fig. 3 shows that the total energy converges exponentially with respect to

. We also note that the total energy converges slightly faster with respect to

for molecules with smaller bond lengths. This reflects the fact that for a given

, the basis set is more complete for a smaller molecule than a larger one because the basis spheres are closer to one another in the smaller molecule.

**Figure 4:** Total energy of the chlorine molecule with a bond length of Å as a function of the maximum angular momentum component $\ell_{\mathrm{max}}$ for different basis-sphere radii and numbers of basis spheres $N_{\scriptstyle\mathrm{bs}}$ . For the three-basis-sphere calculations, two basis spheres are centered on the atoms and a third basis sphere is centered between the atoms. For each spherical-wave calculation, we have used a value of which is the smallest integer such that the cutoff energy exceeds 900 eV. The horizontal solid line corresponds to the total energy obtained from the plane-wave calculation with a cutoff energy of 900 eV.

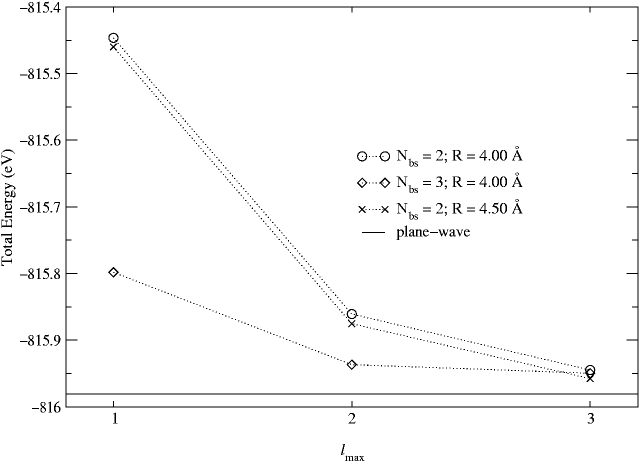
Since the total energy also depends on other parameters such as $l_{\rm {max}}$ and the number of basis spheres $N_{\rm {bs}}$ , we have performed calculations on the chlorine molecule with a bond length of 2.4 Å. The results in Fig. 4 show the convergence of the total energy of the system as a function of $\ell_{\mathrm{max}}$ for different basis-sphere radii

and numbers of basis spheres $N_{\scriptstyle\mathrm{bs}}$ . The rapid convergence of the total energy with respect to $\ell_{\mathrm{max}}$ is evident from the figure. We note that the ``best'' result obtained from the spherical-wave calculation with $N_{\scriptstyle\mathrm{bs}}=2$ ,

4.50 Å, and $\ell_{\mathrm{max}}=3$ gives a total energy of

eV, which lies 0.023 eV above the plane-wave total energy of

eV. This difference, which is due to the incompleteness of the spherical-wave basis set, could be reduced further by increasing the basis-sphere radius

and $\ell_{\mathrm{max}}$ . However, we are content with this accuracy because the error due to the incompleteness of the spherical-wave basis set is only about $3\times 10^{-5}$ of the total energy obtained from the plane-wave calculation. The number of spherical-wave basis functions in this case is only 672, which is a small fraction (0.6%) of 112452, the number of plane waves.

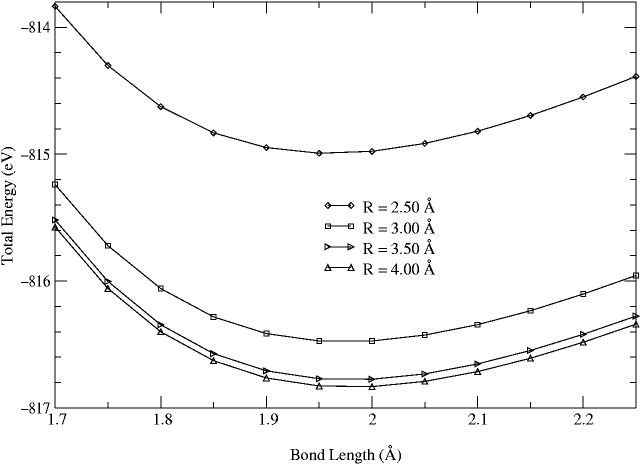
To study the effect of $N_{\scriptstyle\mathrm{bs}}$ , $\ell_{\mathrm{max}}$ and

on the calculated physical properties such as the equilibrium bond length $r_{\mathrm{e}}$ and force constant

, we perform a series of calculations on the chlorine molecule for a range of bond lengths from 1.70 Å to 2.25 Å. A typical result is shown in Fig. 5. The results of the calculations of $r_{\mathrm{e}}$ and

with $\ell_{\mathrm{max}}=$ 1, 2, and 3 are displayed in Tables 1, 2, and 3, respectively. The errors in $r_{\mathrm{e}}$ and

displayed in the columns headed under $\delta r_{\mathrm{e}}$ and $\delta f$ are deduced from the results of the plane-wave calculations.

Table 1: Results for the equilibrium bond length $r_{\mathrm{e}}$ and force constant

of the chlorine molecule with $\ell_{\mathrm{max}}$ = 1. When $N_{\scriptstyle\mathrm{bs}}=2$ , two basis spheres of the same radius

centered on the atoms are used. When $N_{\scriptstyle\mathrm{bs}}=3$ , three basis spheres of the same radius

are used, the third basis sphere being centered between the atoms. The experimental values for $r_{\mathrm{e}}$ and

are 1.9878 Å and 3.23 N/cm, respectively. The plane-wave calculations give values of 1.9661 Å and 3.790 N/cm, respectively, where we have used the same pseudopotentials, Brillouin zone sampling, and cutoff energy.

	$N_{\scriptstyle\mathrm{bs}}$ = 2				$N_{\scriptstyle\mathrm{bs}}$ = 3
(Å)	$r_{\mathrm{e}}$ (Å)	$\delta r_{\mathrm{e}}(\%)$	$\left(\frac{\mathrm{N}}{\mathrm{cm}}\right)$	$\delta f(\%)$	$r_{\mathrm{e}}$ (Å)	$\delta r_{\mathrm{e}}(\%)$	$\left(\frac{\mathrm{N}}{\mathrm{cm}}\right)$	$\delta f(\%)$
2.00	2.0214	2.81	4.880	28.8	1.9565	0.49	4.492	18.5
2.50	2.1240	8.03	2.542	32.9	1.9988	1.66	3.747	1.1
3.00	2.1536	9.54	1.874	50.6	2.0098	2.22	3.557	6.1
3.50	2.1595	9.84	1.772	53.2	2.0123	2.35	3.496	7.8
4.00	2.1623	9.98	1.703	55.1	2.0127	2.37	3.484	8.1
4.50	2.1625	9.99	1.701	55.1	2.0128	2.38	3.481	8.2

In Table 1, the values of $r_{\mathrm{e}}$ and

converge rapidly with respect to

. However, the results with two basis spheres and $\ell_{\mathrm{max}}=1$ shows that the converged results contain unacceptably large systematic errors. The inclusion of a third sphere reduces the errors significantly because the bonding region between the atoms is described better by the third sphere. The results show it is impossible to improve the results simply by enlarging

when $\ell_{\mathrm{max}}=1$ is used.

Table 2: Results for the equilibrium bond length $r_{\mathrm{e}}$ and force constant

of the chlorine molecule with $\ell_{\mathrm{max}}$ = 2. The meanings of

and $N_{\scriptstyle\mathrm{bs}}$ are explained in the caption of Table 1.

	$N_{\scriptstyle\mathrm{bs}}$ = 2				$N_{\scriptstyle\mathrm{bs}}$ = 3
(Å)	$r_{\mathrm{e}}$ (Å)	$\delta r_{\mathrm{e}}(\%)$	$\left(\frac{\mathrm{N}}{\mathrm{cm}}\right)$	$\delta f(\%)$	$r_{\mathrm{e}}$ (Å)	$\delta r_{\mathrm{e}}(\%)$	$\left(\frac{\mathrm{N}}{\mathrm{cm}}\right)$	$\delta f(\%)$
2.00	1.8941	3.66	5.276	39.2	1.9158	2.56	4.591	21.1
2.50	1.9609	0.26	3.959	4.5	1.9537	0.63	4.017	6.0
3.00	1.9733	0.37	3.754	0.9	1.9636	0.13	3.849	1.6
3.50	1.9769	0.55	3.694	2.5	1.9658	0.02	3.802	0.3
4.00	1.9777	0.59	3.673	3.1	1.9663	0.01	3.789	0.0
4.50	1.9778	0.60	3.670	3.2	1.9663	0.01	3.786	0.1

We repeat the calculations for $r_{\mathrm{e}}$ and

with $\ell_{\mathrm{max}}= 2$ , for which the results are presented in Table 2. The converged results with $N_{\scriptstyle\mathrm{bs}}=2$ and $\ell_{\mathrm{max}}= 2$ are better than the converged results with $N_{\scriptstyle\mathrm{bs}}=3$ and $\ell_{\mathrm{max}}=1$ , which indicates the importance of $\ell_{\mathrm{max}}$ over $N_{\scriptstyle\mathrm{bs}}$ for the ``minimal basis set'' calculations. With $\ell_{\mathrm{max}}= 2$ and $N_{\scriptstyle\mathrm{bs}}=2$ , the error of the converged results for $r_{\mathrm{e}}$ and

are

0.50% and 13.6% compared to the experimental values, respectively. These accuracies are acceptable within the LDA.

Table 3: Results for the equilibrium bond length $r_{\mathrm{e}}$ and force constant

of the chlorine molecule with $\ell_{\mathrm{max}}$ = 3.

(Å)	$r_{\mathrm{e}}$ (Å)	$\delta r_{\mathrm{e}}(\%)$	$\left(\frac{\mathrm{N}}{\mathrm{cm}}\right)$	$\delta f(\%)$
2.00	1.8833	4.21	5.212	37.5
2.50	1.9481	0.92	4.128	8.9
3.00	1.9636	0.13	3.860	1.8
3.50	1.9668	0.04	3.792	0.1
4.00	1.9674	0.07	3.777	0.3
4.50	1.9675	0.07	3.773	0.4

Finally in Table 3, we present the values of $r_{\mathrm{e}}$ and

using two basis spheres centered on the atoms $\ell_{\mathrm{max}}=3$ . As expected, the converged values of $r_{\mathrm{e}}$ and

agree very well with the plane-wave results. We note that calculations with $\ell_{\mathrm{max}}=3$ are expensive, since the number of basis functions is almost double that for $\ell_{\mathrm{max}}= 2$ .

Next we calculate the total energy of hydrogen molecule with a bond length of 1.0 Å as a function of the cutoff energy $E_{\mathrm{c}}$ , and the basis sphere radius

, for which the results are displayed in Fig. 6. The total energy converges rather slowly with respect to the cutoff energy because a bare Coulomb potential due to the hydrogen atom is used. Such behavior is also observed in the plane-wave calculations. However, the convergence of energy differences is achieved when the cutoff energy exceeds 800 eV.

We perform a series of total energy calculations on the hydrogen molecule for a range of bond lengths to determine the values of $r_{\mathrm{e}}$ and

. The results are tabulated in Table 4 and show that we can use a value of

as small as 3.00 Å to obtain an accuracy of less than 1% in $r_{\mathrm{e}}$ and

with only two basis spheres. This should be contrasted with the case of the chlorine molecule where with $N_{\scriptstyle\mathrm{bs}}=2$ , $\ell_{\mathrm{max}}= 2$ , and

Å, the values of $r_{\mathrm{e}}$ and

agree only fortuitously with the plane-wave results.

Table 4: Results for the equilibrium bond length $r_{\mathrm{e}}$ and force constant

of the hydrogen molecule with $\ell_{\mathrm{max}}$ = 2. The meanings of

and $N_{\scriptstyle\mathrm{bs}}$ are explained in the caption of Table 1. Cut-off energies above 1000 eV are used. The experimental values for $r_{\mathrm{e}}$ and

are 0.7414 Å and 5.75 N/cm respectively. The equivalent plane-wave calculations give values of 0.7711 Å and 5.197 N/cm, respectively.

	$N_{\scriptstyle\mathrm{bs}}$ = 2				$N_{\scriptstyle\mathrm{bs}}$ = 3
(Å)	$r_{\mathrm{e}}$ (Å)	$\delta r_{\mathrm{e}}(\%)$	$\left(\frac{\mathrm{N}}{\mathrm{cm}}\right)$	$\delta f(\%)$	$r_{\mathrm{e}}$ (Å)	$\delta r_{\mathrm{e}}(\%)$	$\left(\frac{\mathrm{N}}{\mathrm{cm}}\right)$	$\delta f(\%)$
2.00	0.7476	3.05	5.998	15.4	0.7503	2.70	5.865	12.9
2.50	0.7643	0.88	5.420	4.3	0.7668	0.56	5.232	0.7
3.00	0.7695	0.21	5.237	0.8	0.7712	0.01	5.198	0.0
3.50	0.7709	0.03	5.193	0.1
4.00	0.7710	0.01	5.178	0.4

We can explain why, to obtain the same accuracy, the chlorine molecule requires a larger

than the hydrogen molecule. The equilibrium bond length of the hydrogen molecule (which is about 0.74 Å) is smaller than the equilibrium bond length of the chlorine molecule (which is about 1.99 Å). The bonding region between the hydrogen atoms is thus described better by the basis functions because the basis spheres are closer to one another. The hydrogen molecule is also ``smaller'' (in the sense of the extent of the charge distribution) than the chlorine molecule.

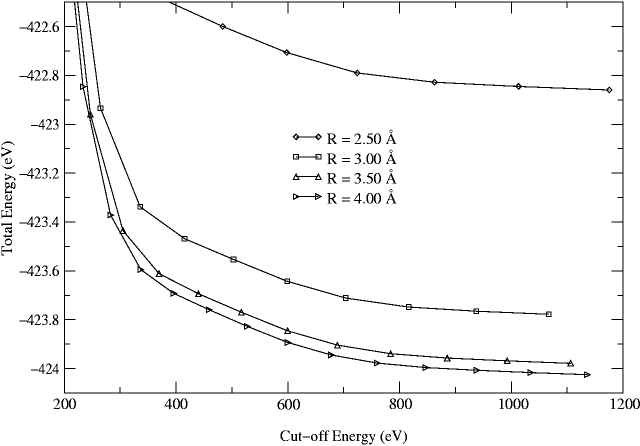
In Fig. 7 we show the total energy of the hydrogen chloride molecule with a bond length of 1.60 Å as a function of the cutoff energy and the radius of the basis sphere. The energy differences converge when the cutoff energy exceeds 800 eV. Calculations are performed to obtain $r_{\mathrm{e}}$ and

, and the results are tabulated in Table 5.

**Figure 7:** Total energy of the hydrogen chloride molecule with a bond length of 1.6 Å as a function of the cutoff energy and the basis sphere radius . Two basis spheres of the same radius centered on the atoms are used. The cubic simulation cell has sides of length 12 Å. $\ell_{\mathrm{max}}= 2$ .

Table 5: Results for the equilibrium bond length $r_{\mathrm{e}}$ and force constant

of the hydrogen chloride molecule with $\ell_{\mathrm{max}}$ = 2. The meanings of

and $N_{\scriptstyle\mathrm{bs}}$ are explained in the caption of Table 1. For the hydrogen chloride molecule, the experimental values for $r_{\mathrm{e}}$ and

are 1.2746 Å and 5.16 N/cm, respectively. The equivalent plane-wave calculations give values of 1.2948 Å and 5.458 N/cm.

	$N_{\scriptstyle\mathrm{bs}}$ = 2				$N_{\scriptstyle\mathrm{bs}}$ = 3
(Å)	$r_{\mathrm{e}}$ (Å)	$\delta r_{\mathrm{e}}(\%)$	$\left(\frac{\mathrm{N}}{\mathrm{cm}}\right)$	$\delta f(\%)$	$r_{\mathrm{e}}$ (Å)	$\delta r_{\mathrm{e}}(\%)$	$\left(\frac{\mathrm{N}}{\mathrm{cm}}\right)$	$\delta f(\%)$
2.00	1.2601	2.68	6.351	16.4	1.2712	1.82	6.030	10.5
2.50	1.2862	0.66	5.683	4.1	1.2885	0.49	5.605	2.7
3.00	1.2926	0.17	5.518	1.1	1.2933	0.12	5.489	0.6
3.50	1.2936	0.09	5.475	0.3	1.2941	0.05	5.461	0.1
4.00	1.2942	0.05	5.466	0.1	1.2946	0.02	5.452	0.1
4.50	1.2945	0.02	5.464	0.1	1.2948	0.00	5.450	0.1

We repeat the $r_{\mathrm{e}}$ and

calculations for the hydrogen chloride molecule, where the radius of the basis sphere centered on the chlorine atom is fixed at 4.00 Å but the radius of the basis sphere centered on the hydrogen atom is varied. The results are presented in Table 6, which shows that we can use a smaller basis sphere of a radius of 2.0 Å centered on the hydrogen atom to obtain an accuracy of less than 1%. It is thus possible to use different basis spheres depending on the atomic species, which is important because this can reduce the computation time significantly.

Table 6: Results for $r_{\mathrm{e}}$ and

of the hydrogen chloride molecule. Two basis spheres are used. The radius of the basis sphere centered on the chlorine atom is fixed at 4.00 Å but the radius

of the basis sphere centered on the hydrogen atom is varied.

(Å)	$r_{\mathrm{e}}$ (Å)	$\delta r_{\mathrm{e}}(\%)$	$\left(\frac{\mathrm{N}}{\mathrm{cm}}\right)$	$\delta f(\%)$
2.00	1.2928	0.15	5.508	0.9
2.50	1.2937	0.08	5.488	0.5
3.00	1.2943	0.04	5.472	0.3
3.50	1.2939	0.07	5.468	0.2
4.00	1.2942	0.05	5.466	0.1

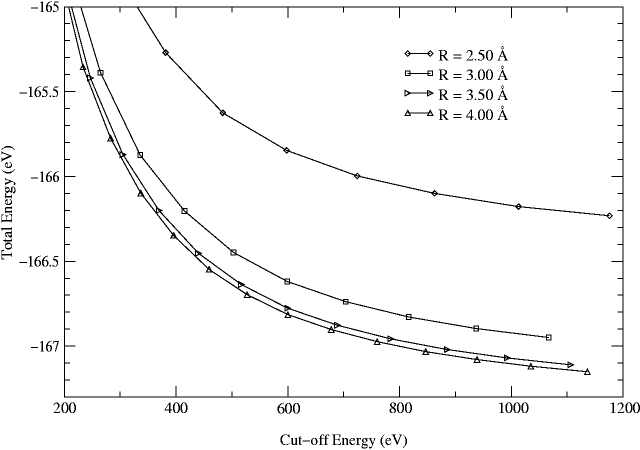
Fig. 8 shows the total energy of the silane molecule with a Si-H bond length of 1.83 Å, as a function of $E_{\mathrm{c}}$ and

. Total energy differences converge for cutoff energies above 800 eV. The results of the calculations of $r_{\mathrm{e}}$ and

(for the breathing mode) are summarized in Table 7. We find that the accuracy is acceptable when

3.00 Å.

Table 7: Results for $r_{\mathrm{e}}$ and

of the silane molecule. Five basis spheres of the same radius

centered on the atoms are used. The cubic simulation cell has sides of length 12 Å. $\ell_{\mathrm{max}}= 2$ . The experimental value of $r_{\mathrm{e}}$ is 1.4798 Å, while the equivalent plane-wave calculations give the values of 1.4910 Å and 11.38 N/cm for $r_{\mathrm{e}}$ and

, respectively.

(Å)	$r_{\mathrm{e}}$ (Å)	$\delta r_{\mathrm{e}}(\%)$	$\left(\frac{\mathrm{N}}{\mathrm{cm}}\right)$	$\delta f(\%)$
2.00	1.4402	3.41	14.640	28.6
2.50	1.4811	0.66	12.010	5.5
3.00	1.4893	0.11	11.523	1.3
3.50	1.4906	0.03	11.415	0.3
4.00	1.4912	0.01	11.382	0.0
4.50	1.4914	0.03	11.379	0.0

We repeat the $r_{\mathrm{e}}$ and

calculations on the silane molecule with the radius of the basis sphere centered on the silicon atom fixed at 4.00 Å, but with the radius

of the basis spheres centered on the hydrogen atoms varied. The results in Table 8 show that an accuracy of 1% can be achieved by using

Å, which is 1 Å larger than the basis spheres centered on the hydrogen atom in the hydrogen chloride molecule calculation (c.f. Table 6).

Table 8: Results for $r_{\mathrm{e}}$ and

of the silane molecule. Five basis spheres centered on the atoms are used. The radius of the basis sphere centered on the silicon atom is fixed at 4.00 Å but the radius

of basis spheres centered on the hydrogen atoms is varied.

(Å)	$r_{\mathrm{e}}$ (Å)	$\delta r_{\mathrm{e}}(\%)$	$\left(\frac{\mathrm{N}}{\mathrm{cm}}\right)$	$\delta f(\%)$
2.00	1.4851	0.40	11.847	4.1
2.50	1.4856	0.36	11.948	5.0
3.00	1.4902	0.05	11.438	0.5
3.50	1.4906	0.03	11.419	0.3
4.00	1.4912	0.01	11.382	0.0

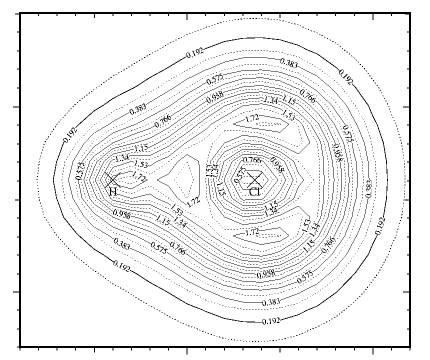
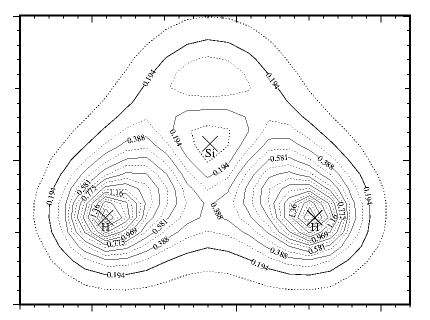
From the pseudo-charge density of the hydrogen chloride molecule (Fig. 9), we observe that the valence electrons are concentrated towards the chlorine atom, as expected from the relative electronegativites of hydrogen and chlorine. This enables us to use a smaller basis sphere centered on the hydrogen atom to obtain accurate results. However, from the pseudo-charge density of the silane (Fig. 10), we observe substantial charge density around the hydrogen atoms, reflecting the fact that hydrogen is more electronegative than silicon. Hence for the silane molecule calculations, the radius of the basis spheres centered on the hydrogen atoms need to be larger than that for hydrogen chloride. These observations lead to the conclusion that the relative electronegativities of neighboring atoms in a calculation should be taken into account when choosing basis sphere radii.

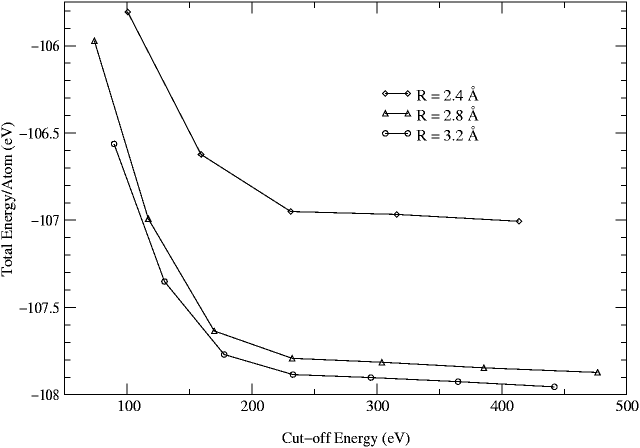
We have chosen bulk crystalline silicon to test the performance of the basis set on an extended system. Fig. 11 shows the total energy per atom for a 64-atom cell of silicon with a lattice parameter of 5.43 Å as a function of the cutoff energy and

. The total energy converges at a cutoff energy of about 250 eV. The rapid convergence of the total energy with respect to

is evident from the figure.

To determine the equilibrium lattice parameter,

, and the bulk modulus,

, we perform a series of calculations on the bulk silicon system for a range of lattice parameters from 5.31 Å to 5.51 Å. The results of the calculations with $\ell_{\mathrm{max}}=$ 1 and 2 are tabulated in Tables 9 and 10, respectively. It is found that even with $\ell_{\mathrm{max}}=1$ , the results with

Å agree quite well with the plane-wave and experiment results. The calculations with $\ell_{\mathrm{max}}= 2$ improve the results slightly. The reason why $\ell_{\mathrm{max}}=1$ calculations give rather good results is because silicon atoms mix the

and

states to form four

orbitals which are obviously well-described by a basis set with $\ell_{\mathrm{max}}=1$ .

Table 9: Results for the equilibrium lattice parameter

and bulk modulus

of the 64-atom bulk crystalline silicon, with $\ell_{\mathrm{max}}=1$ . 64 basis spheres of the same radius

centered on the atoms are used. The experimental values for

and

are 5.43 Å and 100.0 GPa, respectively. The plane-wave calculations, with a cutoff energy of 250 eV, give the results of 5.395 Å and 92.3 GPa, respectively.

(Å)	(Å)	$\delta a(\%)$	(GPa)	$\delta B(\%)$
2.60	5.353	0.78	139.1	50.7
2.80	5.413	0.33	104.5	13.2
3.00	5.445	0.93	97.0	5.1
3.20	5.453	1.08	89.8	2.7

Table 10: Results for the equilibrium lattice parameter

and bulk modulus

of the 64-atom bulk crystalline silicon, with $\ell_{\mathrm{max}}= 2$ . 64 basis spheres of the same radius

centered on the atoms are used.

(Å)	(Å)	$\delta a(\%)$	(GPa)	$\delta B(\%)$
2.60	5.310	1.58	238.0	157.9
2.80	5.353	0.78	129.8	40.6
3.00	5.377	0.33	111.4	20.7
3.20	5.385	0.19	96.2	4.2

Finally we present Table 11 which shows the numbers of basis functions for the spherical-wave and plane-wave basis set calculations. Since in general the number of spherical-wave basis functions is very small for molecules compared to that of plane-wave basis functions, we conclude that spherical-wave basis sets can be used to study molecules and possibly clusters with high efficiency.

Table 11: Numbers of the basis functions required so that the agreement between the results for $r_{\mathrm{e}}$ and

(for molecules); and

and

(for bulk silicon) from the spherical-wave and plane-wave basis set calculations is less than 1%. The numbers of the spherical-wave and plane-wave basis functions are denoted by $N_{\scriptscriptstyle\mathrm{SW}}$ and $N_{\scriptscriptstyle\mathrm{PW}}$ , respectively. For the spherical-wave basis set calculations, the choice of atom-centered and $\ell_{\mathrm{max}}= 2$ is used. $E_{\mathrm{c}}$ is the cutoff energy.

System	$E_{\mathrm{c}}$ (eV)	$N_{\scriptscriptstyle\mathrm{SW}}$	$N_{\scriptscriptstyle\mathrm{PW}}$
Chlorine molecule	800	234	88663
Hydrogen molecule	1000	270	124097
HCl molecule	800	288	88663
Silane molecule	800	720	88663
Bulk silicon	250	4608	10827