

Next: Density-functional calculations
Up: First-principles density-functional calculations using
Previous: Introduction
Origin of the basis set
The spherical-wave basis functions[13] used in this
work are eigenfunctions of the Helmholtz equation
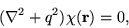 |
(1) |
subject to boundary conditions such that the solutions 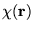 are
nonvanishing only inside a sphere of radius
are
nonvanishing only inside a sphere of radius 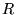 and vanishing
whenever
and vanishing
whenever
 . The eigenfunctions are
. The eigenfunctions are
where
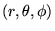 are spherical polar coordinates with origin at
the center of the sphere,
are spherical polar coordinates with origin at
the center of the sphere, 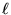 is a non-negative integer and
is a non-negative integer and 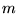 is
an integer satisfying
is
an integer satisfying
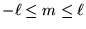 .
. 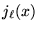 is the
spherical Bessel function of order
is the
spherical Bessel function of order 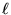 , and
, and
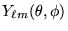 is a spherical harmonic. The eigenvalue
is a spherical harmonic. The eigenvalue 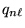 is determined from
the
is determined from
the 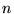 th zero of
th zero of 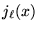 where
where
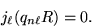 |
(2) |
We note that each eigenfunction in Eq. (2) has an energy
of
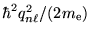 , hence it is possible to
use the concept of cutoff energy to restrict the number of
, hence it is possible to
use the concept of cutoff energy to restrict the number of 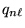 in the expansion of a wavefunction.
in the expansion of a wavefunction.
The real spherical-wave basis functions used in this work are
where 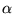 signifies a basis sphere with radius
signifies a basis sphere with radius 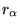 and centered at
and centered at
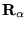 .
.
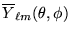 are the real linear combinations of the spherical
harmonics. By construction, all basis functions within a basis sphere
are orthogonal to one another. In general, more than one basis sphere
is needed to expand a wavefunction
are the real linear combinations of the spherical
harmonics. By construction, all basis functions within a basis sphere
are orthogonal to one another. In general, more than one basis sphere
is needed to expand a wavefunction
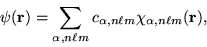 |
(3) |
where
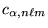 are the associated coefficients.
For most systems tested in this work, we have
used one basis sphere per atom,
where the basis spheres are centered
on the atoms. For some systems we have increased the number of
basis spheres by placing basis spheres between the atoms.
In principle it is possible to use two or more basis spheres of
different radii centered
on the same atom, but this arrangement has not been studied in this work.
We note that even
though the basis functions belonging to different basis spheres are
generally nonorthogonal, one of the main advantages of this basis set
is that it is possible to analytically evaluate[13] the
overlap matrix elements
are the associated coefficients.
For most systems tested in this work, we have
used one basis sphere per atom,
where the basis spheres are centered
on the atoms. For some systems we have increased the number of
basis spheres by placing basis spheres between the atoms.
In principle it is possible to use two or more basis spheres of
different radii centered
on the same atom, but this arrangement has not been studied in this work.
We note that even
though the basis functions belonging to different basis spheres are
generally nonorthogonal, one of the main advantages of this basis set
is that it is possible to analytically evaluate[13] the
overlap matrix elements
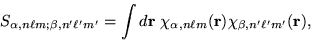 |
(4) |
and kinetic energy matrix elements
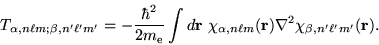 |
(5) |
We also note that the matrix elements for the nonlocal
pseudopotentials in the Kleinman-Bylander[19] form can
also be evaluated analytically by first expanding the projectors in
the spherical-wave basis set.


Next: Density-functional calculations
Up: First-principles density-functional calculations using
Previous: Introduction
Peter D. Haynes
2002-10-31