

Next: Psinc functions
Up: Preconditioned iterative minimization
Previous: General formalism
The case of an orthogonal basis
In the special case of an orthogonal basis  there
is no distinction between covariant and contravariant quantities with
respect to the expansion coefficients of this basis, and
as such we use Latin suffixes to denote them:
there
is no distinction between covariant and contravariant quantities with
respect to the expansion coefficients of this basis, and
as such we use Latin suffixes to denote them:
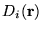 . In this case, Eq. (24)
becomes
. In this case, Eq. (24)
becomes
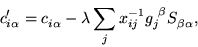 |
(30) |
where we have defined
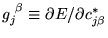 .
.
Let 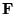 be that unitary transformation which
diagonalises the (Hermitian) matrix
be that unitary transformation which
diagonalises the (Hermitian) matrix 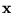 , i.e.,
, i.e.,
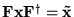 ,
where
,
where
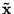 is a matrix with eigenvalues
is a matrix with eigenvalues
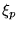 on its diagonal:
on its diagonal:
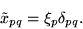 |
(31) |
Denoting transformed variables by
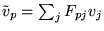 , we apply
, we apply 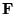 to Eq. (30) to
obtain
to Eq. (30) to
obtain
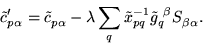 |
(32) |
From Eq. (31) we see that
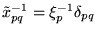 is diagonal, hence
Eq. (32) becomes
is diagonal, hence
Eq. (32) becomes
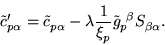 |
(33) |
In other words, for the case of an orthogonal basis 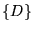 , the
transformed gradient is preconditioned by premultiplying by a
diagonal matrix of inverse eigenvalues
, the
transformed gradient is preconditioned by premultiplying by a
diagonal matrix of inverse eigenvalues
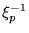 . Post-multiplication by the overlap matrix
. Post-multiplication by the overlap matrix
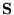 is still present in order to account for the
nonorthogonality of the localized functions
is still present in order to account for the
nonorthogonality of the localized functions 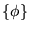 .
.


Next: Psinc functions
Up: Preconditioned iterative minimization
Previous: General formalism
Arash Mostofi
2003-10-28
![]() be that unitary transformation which
diagonalises the (Hermitian) matrix
be that unitary transformation which
diagonalises the (Hermitian) matrix ![]() , i.e.,
, i.e.,
![]() ,
where
,
where
![]() is a matrix with eigenvalues
is a matrix with eigenvalues
![]() on its diagonal:
on its diagonal:
![]() , we apply
, we apply ![]() to Eq. (30) to
obtain
to Eq. (30) to
obtain