

Next: Orthogonal basis
Up: Preconditioned iterative minimization
Previous: Principles
General formalism for kinetic energy preconditioning
We introduce a positive-definite model Hamiltonian 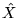 and write
the energy of the system that it describes as
and write
the energy of the system that it describes as
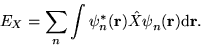 |
(15) |
We proceed to derive exact expressions for preconditioning the
minimization of Eq. (15). For
suitable choice of 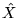 , these same expressions may be
used to improve the condition number for minimizing the true energy
Eq. (3). It is worth noting that all of the occupation
numbers
, these same expressions may be
used to improve the condition number for minimizing the true energy
Eq. (3). It is worth noting that all of the occupation
numbers 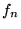 for the model system have been set to unity. This
amounts to an additional occupancy preconditioning,
first introduced by Gillan [36] in the context of
metallic systems and then by Marzari et
al. [29] in the general framework of
ensemble density-funtional theory.
for the model system have been set to unity. This
amounts to an additional occupancy preconditioning,
first introduced by Gillan [36] in the context of
metallic systems and then by Marzari et
al. [29] in the general framework of
ensemble density-funtional theory.
Following along the same lines as in Section 2,
defining
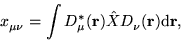 |
(16) |
and substituting this, Eq. (4) and Eq. (10) into
Eq. (15) we obtain
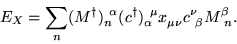 |
(17) |
It is at this point that a tensorially incorrect ``diagonal
approximation'' is made in Ref. [21].
In our notation, this would be given by
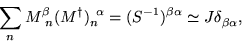 |
(18) |
where 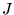 is some constant, and the first equality follows from
Eq. (6). We do not make this unnecessary
approximation.
is some constant, and the first equality follows from
Eq. (6). We do not make this unnecessary
approximation.
Formally, as it has been defined to be positive-definite, the matrix
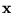 may be expressed in terms of its unique Cholesky factor
may be expressed in terms of its unique Cholesky factor
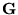 [37]:
[37]:
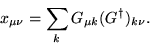 |
(19) |
Substituting this into Eq. (17) gives
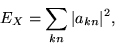 |
(20) |
where the new variables 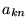 which
make the energy surface spherical are given by
which
make the energy surface spherical are given by
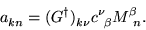 |
(21) |
In a steepest
descents procedure, although the following easily generalises to
the conjugate gradients method, a line minimization is performed along
the steepest descents search direction to find the new values of the
coefficients 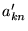 :
:
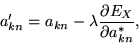 |
(22) |
where 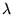 is chosen to minimize the energy. We wish to
minimize the energy with respect to the coefficients
is chosen to minimize the energy. We wish to
minimize the energy with respect to the coefficients
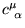 , yet the functional is spherical (and hence
preconditioned) in the new coefficients
, yet the functional is spherical (and hence
preconditioned) in the new coefficients 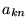 . In order to find the
new values
. In order to find the
new values
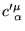 of the coefficients
of the coefficients
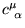 that minimize the energy, we use the chain rule to write
that minimize the energy, we use the chain rule to write
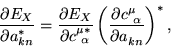 |
(23) |
and from this, and Eqs. (21)-(22),
it may be shown that
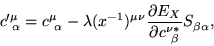 |
(24) |
where we have used the relations
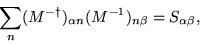 |
(25) |
and
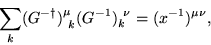 |
(26) |
obtained from Eqs. (6) and
(19), respectively.
Choosing the model Hamiltonian 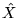 introduced in
Eq. (14), and defining
introduced in
Eq. (14), and defining
Eq. (24) becomes
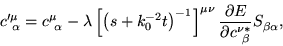 |
(29) |
where, following the discussion in Section 3,
we have replaced the model energy 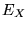 with the true energy
with the true energy 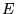 .
We see from Eq. (29) that preconditioning is
effected by premultiplying the steepest descent gradient by the matrix
.
We see from Eq. (29) that preconditioning is
effected by premultiplying the steepest descent gradient by the matrix
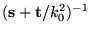 and postmultiplying it by
and postmultiplying it by
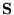 .
.


Next: Orthogonal basis
Up: Preconditioned iterative minimization
Previous: Principles
Arash Mostofi
2003-10-28
![]() may be expressed in terms of its unique Cholesky factor
may be expressed in terms of its unique Cholesky factor
![]() [37]:
[37]:
![]() :
:
![]() introduced in
Eq. (14), and defining
introduced in
Eq. (14), and defining