

Next: Results
Up: Preconditioned iterative minimization
Previous: Orthogonal basis
Preconditioning and periodic sinc functions
We consider a unit cell (which we shall refer to as the simulation
cell) with primitive lattice vectors
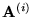 (
(
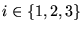 ), volume
), volume
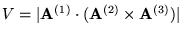 , and
, and
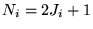 grid points along
direction
grid points along
direction 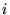 , where the
, where the 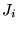 are integers. Our basis set
is composed of periodic bandwidth-limited
delta-functions [20], from here
on referred to as periodic sinc or psinc functions, defined as
the following finite sum of plane waves:
are integers. Our basis set
is composed of periodic bandwidth-limited
delta-functions [20], from here
on referred to as periodic sinc or psinc functions, defined as
the following finite sum of plane waves:
where 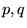 and
and 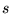 are integers, and the
are integers, and the
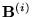 are the
reciprocal lattice vectors:
are the
reciprocal lattice vectors:
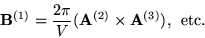 |
(35) |
and the
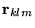 are the grid points of the simulation cell,
are the grid points of the simulation cell,
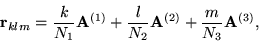 |
(36) |
where 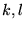 , and
, and 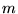 are integers:
are integers:
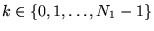 , and
similarly for
, and
similarly for 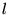 and
and 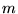 . There is one psinc function centered on each
grid point of the simulation cell.
. There is one psinc function centered on each
grid point of the simulation cell.
The name ``periodic sinc'', or psinc, has been chosen to
reflect the connection that this function has with the familiar
``cardinal sine'' or sinc function. The sinc function is a continuous
integral of plane waves with unit coefficients up to a maximum cut-off
frequency.
The psinc function differs only in that this continous integral is
replaced by a finite sum over the reciprocal lattice vectors of the
simulation cell, as in Eq. (34). As a result,
whereas the sinc function decays to zero at infinity, the
psinc function is cell-periodic, namely
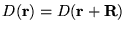 , where
, where 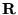 is any lattice
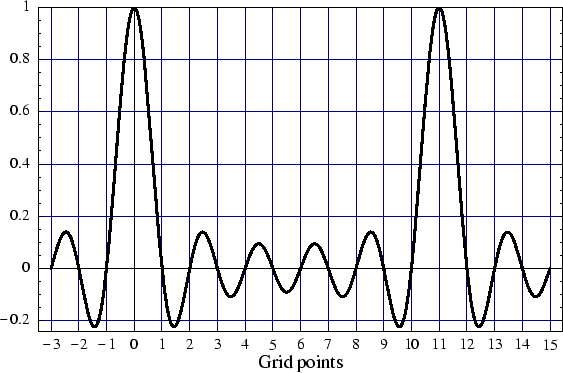
vector. Fig. 1 shows a one-dimensional analogue
of a single psinc function.
is any lattice
vector. Fig. 1 shows a one-dimensional analogue
of a single psinc function.
Figure 1:
One-dimensional analogue of a single periodic sinc, or
psinc function, centered on the origin. In this example the
simulation cell is eleven grid points in length.
|
|
From this point onward, for simplicity of notation, we write the
psinc functions introduced in Eq. (34) as
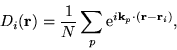 |
(37) |
where
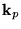 denotes a reciprocal lattice point,
denotes a reciprocal lattice point,
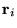 denotes a grid point of the simulation cell, and
denotes a grid point of the simulation cell, and
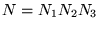 is the total number of grid points in the
simulation cell.
is the total number of grid points in the
simulation cell.
Using the same model Hamiltonian 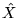 given by
Eq. (14) along with the definitions presented
in Eqs. (27) and (28), we
write
given by
Eq. (14) along with the definitions presented
in Eqs. (27) and (28), we
write
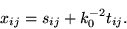 |
(38) |
As shown in the Appendix, the psinc functions are
orthogonal,
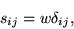 |
(39) |
and the matrix elements of 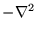 in the psinc basis are given
by
in the psinc basis are given
by
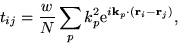 |
(40) |
where 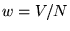 , the grid point weight, and
, the grid point weight, and
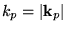 .
.
The operator 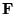 which diagonalises
which diagonalises
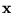 is none other than the discrete Fourier transform:
is none other than the discrete Fourier transform:
where the 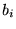 are values on the real space grid and the
are values on the real space grid and the
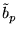 are values on the reciprocal space grid.
Using these definitions, along with
Eqs. (38)-(40) and
Eq. (47), it is a simple matter to show that
are values on the reciprocal space grid.
Using these definitions, along with
Eqs. (38)-(40) and
Eq. (47), it is a simple matter to show that
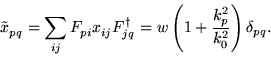 |
(43) |
Thus the eigenvalues 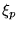 of
of
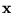 are given by
are given by
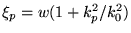 .
Substituting this into Eq. (33) gives the final
expression for our preconditioned line minimization:
.
Substituting this into Eq. (33) gives the final
expression for our preconditioned line minimization:
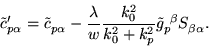 |
(44) |


Next: Results
Up: Preconditioned iterative minimization
Previous: Orthogonal basis
Arash Mostofi
2003-10-28
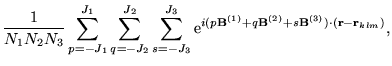
![]() , where
, where ![]() is any lattice
vector. Fig. 1 shows a one-dimensional analogue
of a single psinc function.
is any lattice
vector. Fig. 1 shows a one-dimensional analogue
of a single psinc function.
![]() given by
Eq. (14) along with the definitions presented
in Eqs. (27) and (28), we
write
given by
Eq. (14) along with the definitions presented
in Eqs. (27) and (28), we
write
![]() which diagonalises
which diagonalises
![]() is none other than the discrete Fourier transform:
is none other than the discrete Fourier transform: