

Next: Principles
Up: Preconditioned iterative minimization
Previous: Introduction
Formulation of the problem
A system of noninteracting particles in a potential
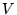 is described by
is described by
![\begin{displaymath}
\hat{H}\psi_{n}(\mathbf{r}) = \left[
-\frac{\hbar^{2}}{2m}\...
...ght] \psi_{n}(\mathbf{r}) = \epsilon_{n} \psi_{n}(\mathbf{r}),
\end{displaymath}](img11.png) |
(1) |
where 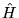 is the single-particle Hamiltonian of the system, with
energy eigenvalues
is the single-particle Hamiltonian of the system, with
energy eigenvalues 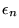 and corresponding eigenstates
and corresponding eigenstates
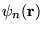 . The eigenstates satisfy the
orthogonality constraints given by
. The eigenstates satisfy the
orthogonality constraints given by
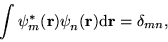 |
(2) |
for all 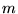 and
and 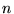 . For instance, within the Kohn-Sham scheme of
density-functional
theory [22,23,24],
. For instance, within the Kohn-Sham scheme of
density-functional
theory [22,23,24], 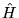 is
the Kohn-Sham Hamiltonian and
is
the Kohn-Sham Hamiltonian and 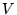 is the effective potential.
is the effective potential.
The total band-structure energy is given by
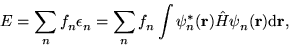 |
(3) |
where 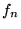 is the occupancy of state
is the occupancy of state
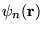 [25]: at the energy minimum, all states
below and above the Fermi-level have occupancy unity and zero,
respectively.
[25]: at the energy minimum, all states
below and above the Fermi-level have occupancy unity and zero,
respectively.
In the case of linear-scaling calculations, the 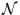 lowest
extended eigenstates
lowest
extended eigenstates
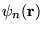 (
(
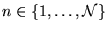 ) are expressed in terms of a set of
) are expressed in terms of a set of
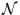 localized functions
localized functions
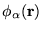 (
(
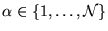 ) that are generally
nonorthogonal:
) that are generally
nonorthogonal:
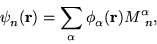 |
(4) |
where 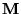 is a square (
is a square (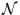 by
by 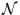 ),
nonsingular matrix of coefficients, and
),
nonsingular matrix of coefficients, and 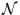 can be equal to
or greater than the
number of occupied eigenstates. The overlap matrix
can be equal to
or greater than the
number of occupied eigenstates. The overlap matrix
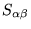 of the localized functions
of the localized functions
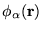 is
is
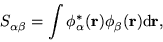 |
(5) |
and on substitution of Eq. (4) into the orthogonality
relation given by Eq. (2) we find that
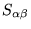 satisfies
satisfies
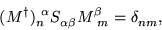 |
(6) |
where a distinction has been made between
contravariant and covariant
quantities [26,27] through the use of
superscript and subscript Greek suffixes, respectively.
Substituting Eq. (4) into the energy expression of
Eq. (3), and defining
the band-structure energy becomes
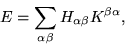 |
(9) |
where
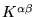 is referred to as the density
kernel [28].
is referred to as the density
kernel [28].
We consider the localized functions
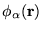 to
be represented in terms of a basis
to
be represented in terms of a basis
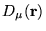 as follows:
as follows:
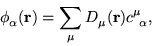 |
(10) |
for some coefficients
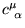 . As the basis functions
. As the basis functions
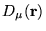 may be in general nonorthogonal, the tensor
properties must be taken into account through the use of superscript
and subscript Greek suffixes.
may be in general nonorthogonal, the tensor
properties must be taken into account through the use of superscript
and subscript Greek suffixes.
Defining
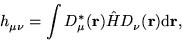 |
(11) |
and using Eqs. (7)-(10),
the energy may be written as
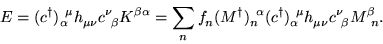 |
(12) |
Suffixes 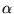 and
and 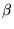 run over
the localized functions
run over
the localized functions 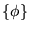 ,
, 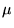 and
and 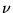 run over the
basis functions
run over the
basis functions 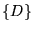 and
and 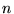 runs over the extended orthogonal
orbitals
runs over the extended orthogonal
orbitals 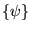 . We have adopted the
Einstein summation convention for all repeated Greek suffixes, and
continue to do so from here on.
. We have adopted the
Einstein summation convention for all repeated Greek suffixes, and
continue to do so from here on.
It is both convenient and physically meaningful to perform the
minimization of the energy functional in two nested loops, as in the
ensemble density-functional method of Marzari et
al. [29]: in the inner loop
we minimize the energy with respect to the elements of the density
kernel
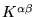 using one of a number of
methods [30,31,32] to impose the
constraint that the ground state density matrix be idempotent and give
the correct number of electrons; in the outer loop we optimize the
localized functions
using one of a number of
methods [30,31,32] to impose the
constraint that the ground state density matrix be idempotent and give
the correct number of electrons; in the outer loop we optimize the
localized functions
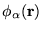 with respect to their
coefficients
with respect to their
coefficients
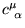 in the basis
in the basis
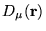 [16].
[16].


Next: Principles
Up: Preconditioned iterative minimization
Previous: Introduction
Arash Mostofi
2003-10-28
![]() lowest
extended eigenstates
lowest
extended eigenstates
![]() (
(
![]() ) are expressed in terms of a set of
) are expressed in terms of a set of
![]() localized functions
localized functions
![]() (
(
![]() ) that are generally
nonorthogonal:
) that are generally
nonorthogonal:
![]() to
be represented in terms of a basis
to
be represented in terms of a basis
![]() as follows:
as follows:
![]() using one of a number of
methods [30,31,32] to impose the
constraint that the ground state density matrix be idempotent and give
the correct number of electrons; in the outer loop we optimize the
localized functions
using one of a number of
methods [30,31,32] to impose the
constraint that the ground state density matrix be idempotent and give
the correct number of electrons; in the outer loop we optimize the
localized functions
![]() with respect to their
coefficients
with respect to their
coefficients
![]() in the basis
in the basis
![]() [16].
[16].