The Ewald summation method[55, 56, 57] is a technique for evaluating the potential, subject to periodic boundary conditions, due to a lattice of point charges, plus a screening background,
![]()
where ![]() is the position of the n
is the position of the n ![]() charge in the
simulation cell and
charge in the
simulation cell and ![]() is the set of supercell translation
vectors. To solve Poisson's equation for the Ewald potential,
is the set of supercell translation
vectors. To solve Poisson's equation for the Ewald potential,
![]()
due to the above charge density, the density is split up into two
components, the background charge and the array of delta functions.
An array of Gaussian functions, centred at ![]() is
added to each component of the Ewald charge density. The Gaussians
are normalised to ensure that both of the individual components of the
Ewald charge density are neutral. The two charge density components
can be written as
is
added to each component of the Ewald charge density. The Gaussians
are normalised to ensure that both of the individual components of the
Ewald charge density are neutral. The two charge density components
can be written as
![]()
where
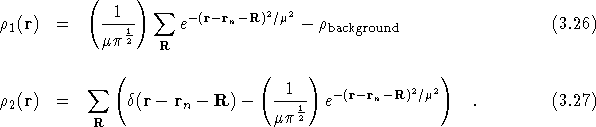
These charge densities are schematically represented in one dimension
in figure ![]() .
.
Figure: Schematic representation of the two components of the
Ewald charge density. Blue indicates positive charge and red negative
charge.
The potential due to ![]() is most conveniently calculated
in reciprocal space.
is most conveniently calculated
in reciprocal space. ![]() has non-zero Fourier
components on supercell reciprocal lattice vectors,
has non-zero Fourier
components on supercell reciprocal lattice vectors, ![]() , given by
, given by
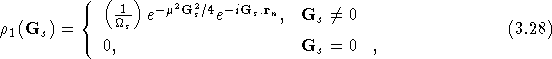
where ![]() is the volume of the supercell. Solving the
corresponding reciprocal space version of Poisson's equation,
is the volume of the supercell. Solving the
corresponding reciprocal space version of Poisson's equation,
![]() , gives
, gives
![]()
To calculate ![]() , the potential due to the array of
point charges minus the screening Gaussians, evaluation in real space
is more convenient since the coefficients in the Fourier expansion of
a periodic array of delta functions do not decay for large
, the potential due to the array of
point charges minus the screening Gaussians, evaluation in real space
is more convenient since the coefficients in the Fourier expansion of
a periodic array of delta functions do not decay for large ![]() vectors. The resultant potential is the summed potential of the delta
function point charges minus the sum of potentials due to the Gaussian
charge distributions. One can show that the potential of the Gaussian
charge distribution is given by
vectors. The resultant potential is the summed potential of the delta
function point charges minus the sum of potentials due to the Gaussian
charge distributions. One can show that the potential of the Gaussian
charge distribution is given by
![]()
where the error function is defined as
![]()
Consequently, the real space sum generating ![]() is
is
![]()
where the last term, ![]() , is added so that
the average potential in the supercell is zero. Combining the
reciprocal space sum for
, is added so that
the average potential in the supercell is zero. Combining the
reciprocal space sum for ![]() and the real space sum for
and the real space sum for
![]() gives the final result for
gives the final result for ![]()
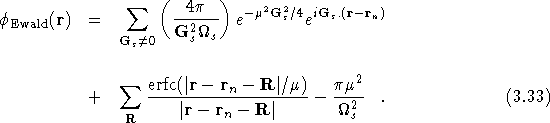
The value of ![]() is independent of the half
width,
is independent of the half
width, ![]() , of the Gaussian charges. However, the value of
, of the Gaussian charges. However, the value of ![]() affects the speed of convergence of the above real and reciprocal
space sums.
affects the speed of convergence of the above real and reciprocal
space sums.
The full potential of a simulation cell containing N electrons and M ions is found by superposing all the potentials for each charge component, since the full charge distribution is the superposition of all the point charges and their cancelling backgrounds,
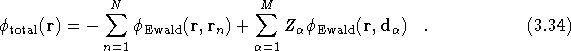
Therefore ![]() , as defined in Eq.(
, as defined in Eq.(![]() ) is
given by
) is
given by
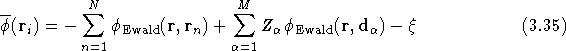
where
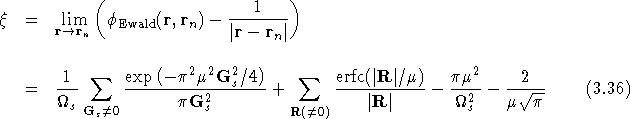
is the self-image interaction, i.e. the potential at the unit point
charge due to its own background and array of
images. ![]() can be found in exactly
the same way and the total electrostatic energy per simulation cell
can then be written as
can be found in exactly
the same way and the total electrostatic energy per simulation cell
can then be written as
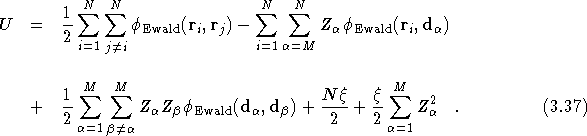
The charge neutrality of the simulation cell dictates that

Therefore the above expression for U is easily simplified to
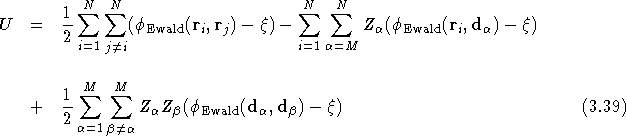
In QMC solid calculations, the ionic coordinates are fixed throughout the calculation. Therefore the contribution to the total energy from the ion-ion Coulomb interaction need only be evaluated once at the beginning of the simulation.
As each of the electrons are moved in turn in a VMC calculation, the contribution to the total energy from the electron-electron and electron-ion Coulomb interactions needs to be recalculated for each electron after it is moved.