We now need to extend the above analysis to calculate the potential in the simulation cell when it is just one of an infinite number of periodically repeated, identical simulation cells making up a bulk solid, as in a supercell calculation. The infinite summations of Coulomb potentials from all the charges in the infinite system are only conditionally convergent. It is therefore easier to solve Poisson's equation, again just for the simulation cell, but now imposing periodic boundary conditions to build in the effect of all the periodic images of the simulation cell.
Let us first consider such a crystal with a smoothly varying charge
density. The charge density has the periodicity of the primitive
lattice and can therefore be written as a Fourier expansion in the
reciprocal primitive lattice vectors, 
, as follows
This charge density generates a potential, 
, satisfying
Poisson's equation, Eq.(
). We can also expand the potential
in a Fourier Series to obtain a reciprocal space version of Poisson's equation,
Hence one can solve for
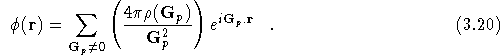
Eq.() is only soluble provided
, which implies that one can only solve Poisson's
equation for an infinite periodic system if each unit cell is neutral.
In this case, the value of 
is completely arbitrary,
corresponding to a constant shift in potential which does not affect
the potential energy of the system as a whole because it applies in
equal and opposite amounts to the positive and negative charges in the
system. The solution of Poisson's equation subject to periodic
boundary conditions is unique up to an arbitrary constant. This can
be demonstrated as follows. Suppose that there were two different
periodic solutions, 
and 
, to
Poisson's equation. The difference between these two solutions,
also satisfies the periodic boundary conditions. must
also satisfy Laplace's equation
everywhere within the simulation cell and so must be a
constant throughout the simulation cell as this is the only periodic
solution of Laplace's equation. Therefore the two solutions to
Poisson's equation are indeed the same to within an arbitrary
constant.
It has therefore been shown that the potential due to a smooth charge density can easily be evaluated in reciprocal space. However, in a QMC calculation, the instantaneous positions of the electrons are represented in real space by a set of delta functions. This array of delta functions cannot be represented by a convergent Fourier series in the same way that a smooth charge density can, and so the above method for evaluating the potential breaks down. The method of calculating the potential due to such a charge density of point charges that has been traditionally used in QMC calculations is Ewald summation. This method is described in the following section.
