Before treating the full supercell system, let us consider the Coulomb energies of the particles in an isolated simulation cell[3]. This is exactly the situation one would be faced with when studying clusters of atoms within QMC.
The cell contains N electrons each with charge -1 at positions
and M nuclei with charges 
at positions
. When the Born-Oppenheimer approximation is used,
the positions of the nuclei act only as parameters in the electronic
Hamiltonian. This Hamiltonian can be written as
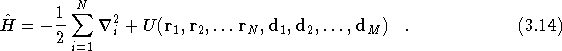
For an isolated simulation cell, the term U is simply a superposition of the Coulomb energies for each particle,
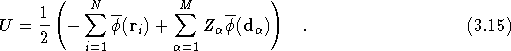
The Coulomb energy for each particle is the result of interactions
with all the other charges. There is no self-interaction and so the
electrostatic potentials, 
, which appear in
the equation for U, are the full Coulomb potentials, 
,
minus the Coulomb potential of the particle situated at
The full Coulomb potential, , may be calculated by solving
Poisson's equation,
where 
is the charge density, and the
boundary condition is that the potential tends to zero as
.
