The evaluation of non-local pseudopotentials within the QMC solid
codes is dealt with in detail in chapter 
.
Optimising wavefunctions with respect to these non-local
pseudopotentials is discussed in chapter . In
chapters and , DMC calculations
involving a non-local pseudopotential to describe silicon are
reported. The use of such non-local pseudopotentials within DMC is a
problem that is yet to be completely resolved. Here we discuss the
approximations used later in the thesis to try and deal with this
problem.
Consider Eq.(), in which a pseudopotential is used
to describe the valence electrons in a system;
We can divide the full valence Hamiltonian, 
, into
a local and non-local part
where 
includes the kinetic energy, the local part
of the pseudopotential and the Coulomb interaction, and W includes the
non-local part of the pseudopotential. The diffusion-drift equation for f,
Eq.(), can be split into two terms representing the local and
non-local parts of the Hamiltonian
The first three terms on the left hand side of Eq.()
can be interpreted as a local diffusion, drifting and branching
process. However, the fourth term represents the operation of the
non-local pseudopotential on the unknown wavefunction, 
,
producing non-local branching. In the DMC calculations described in
chapters and , we have used
the ``locality approximation'' which was introduced by
Christiansen[38, 39, 40]
and recently applied by Mitas[41, 42] to the
problem of the unknown wavefunction in Eq.(). In this
approximation, the non-local pseudopotential acts not on the unknown
wavefunction, , but on the guiding wavefunction, 
,
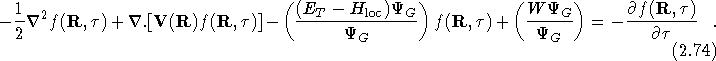
One is then free to impose the fixed-node approximation in the same
way as before. In fact, when using the above local model potential,
it is important that the fixed node approximation is applied as this
steers the random walk away from the nodes of , where there will
generally be divergences in the local model potential. Without the
fixed node approximation, these divergences would cause large
fluctuations in the population of diffusing particles.
It should be noted that within the ``locality approximation'', it is
no longer generally true that the DMC estimate of the energy is an
upper bound to the true groundstate energy. It must always be less
than the VMC energy and it has been shown, [42] that
the DMC energy converges quadratically to the exact groundstate energy
as the guiding function approaches the true groundstate
wavefunction.
