Performing DMC Calculations on Parallel Computers

The argument for performing DMC calculations on a parallel computer is even more compelling than for VMC calculations, because DMC calculations require approximately an order of magnitude more CPU time than the equivalent VMC calculation.

As with VMC calculations, the DMC algorithm is intrinsically parallel. In the algorithm outlined in section , an ensemble of walkers is used to evaluate the local energy of the guiding function, , at each time step of the simulation. In our parallel version of the DMC algorithm, this ensemble of walkers is distributed across all NNODES nodes of the parallel machine. Each node is responsible for performing stages (2)-(8) of the algorithm (the diffusion, drift and creation/annihilation of walkers) on its own subset of the total ensemble of walkers.

After all the walkers have been advanced for a block of time steps, the mean energy across all the walkers on all the nodes is used to update the trial energy as in stage (11) of the algorithm.

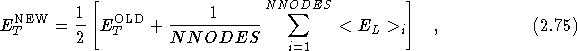
where is the accumulated local energy of the subset of walkers on the i node.

The renormalisation of the number of walkers at the end of a block is performed across all the nodes in the following way.

1. The number of `live' walkers summed across all the nodes, , at the end of the block is compared with the original number, .
2. If there are too many walkers then walkers are selected at random and deleted. If there are too few walkers then walkers are chosen at random and copied.
3. The walkers are the redistributed across the nodes so that there are walkers on each node at the start of the next block.

It is important to try and keep the number of walkers on each node equal, i.e. to `load balance' the algorithm efficiently. The efficiency of the algorithm at any one time step is determined by

where is the total number of walkers across all the nodes and is the number of walkers on the node which at that particular time step has the largest number of `live' walkers. The efficiency of the algorithm can therefore be improved in two ways,

1. Keep the number of walkers as well `balanced' across the nodes as possible.
2. Increase the average number of walkers per node, .

To understand (2), consider the case where at one time step all the nodes contain the same number of walkers. At the end of that step, one of the walkers on one of the nodes is duplicated by the branching process. That node then contains one more walker than all the other nodes. Therefore, at the next time step, all the other nodes will have to wait while that node moves its extra walker. The fraction of time wasted decreases as the average number of walkers per node increases. Option (1), involves balancing the time involved in redistributing walkers across the nodes with the time wasted due to reduced efficiency of the algorithm. On modern MPP machines such as the Cray T3D, the time to redistribute a walker is very small and so we choose to redistribute the walkers at the end of every time step. This places a lower bound on the efficiency of

In other words any one node can never have more than one more walker than any other node. For the DMC calculations reported on in this thesis, there are typically 10 walkers per node, yielding an average efficiency of approximately 95%.

The parallel DMC algorithm requires a set of equilibrated configurations as an input, in the same way as the serial DMC algorithm. These configurations are produced by instructing each node in the parallel VMC algorithm to write out an equilibrated ensemble of configurations.