Let us now repeat the above analysis using the enhanced expression for
the electron-electron interaction of Eq.(), designed to
remove the effect of the unwanted periodic array of additional
electrons. The HF equivalent of this energy expression is
The resultant HF equations obtained from minimising 
in
Eq.() with respect to the 
are exactly the
same as Eq.(), obtained from the original energy
expression. The eigenvalues, 
, are therefore also exactly
the same as those given in Eq.(). However, if one
considers the change in the total energy on adding an electron to
state k, using the energy expression in Eq.(), one
obtains a similar expression to Eq.() but without the
term arising from the interaction between the 
electron and
its images, i.e.
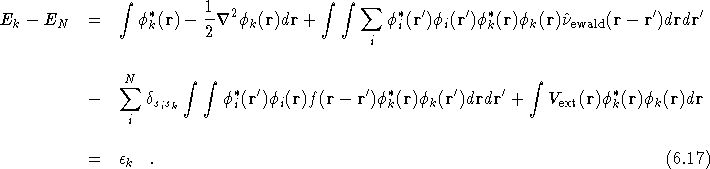
Therefore, when using the enhanced version of the electron-electron
interaction from Eq.(), one recovers the standard version of
Koopmans' theorem where the eigenstates of the HF equations correspond
to the excitation energies of the system,
and hence the HF energy gap, obtained using the expression for the
electron-electron interaction of Eq.() is given
by
The comparison of the two energy expressions,
Eq.() and Eq.(), within HF
theory can therefore be summarised as follows. The enhanced version
of the electron-electron interaction, Eq.(), improves
over the original expression in two ways, (i) it removes the self-term
due to the interaction of an electron and its images, (ii) it recovers
a proper version of Koopmans' theorem. Both these results provide
additional support for the use of the enhanced interaction,
Eq.(), in the following QMC calculations.
