Within the HF approximation the interaction of
Eq.() leads to the following expression for the
total energy;
where 
is the spin of the 
electron. The two charge
densities in the second (Hartree) term have been chosen to be the same
for simplicity. In the case of HF calculations performed using fixed
LDA orbitals, this corresponds to using the LDA charge density as the
`input' charge density to the interaction in the same way as is done
for VMC calculations.
The resultant HF equations obtained from minimising 
in
Eq.() with respect to the 
are
Therefore the eigenvalue, 
, is given by
Eqs.() and () yield an analogue of Koopmans' theorem for adding an electron
where 
is the total energy of the system with an extra electron
added into the 
orbital. Note that if 
is replaced with the standard 
we
retrieve the standard Koopmans' theorem.
The equivalent expression for removing an electron is
and therefore the HF energy gap, obtained using the expression for the
electron-electron interaction of Eq.() is given
by
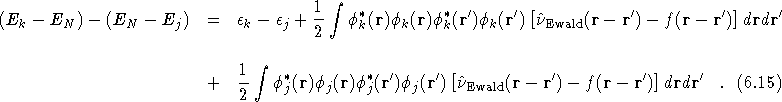
Koopmans' theorem has therefore been modified. The interaction is, in a sense, including self-interaction like terms.
