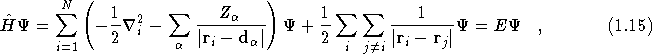
Density Functional theory[7, 8] is a formally exact theory based on the charge density of a system. Kohn-Sham Density Functional theory[9] is a formally exact one-electron theory. Working within the Born-Oppenheimer approximation, the many-body Schrödinger equation,
where 
is the many-body wavefunction, is replaced by a
set of N one-electron equations of the form
where 
is a single-electron wavefunction. These
one-electron equations contain a potential 
produced by
all the ions and the electrons. Density Functional theory properly
includes all parts of the electron-electron interaction, i.e. the
Hartree potential
where 
is the charge density of all the electrons, a potential
due to exchange and correlation effects, 
, and the
external potential due to the ions, 
,
Hohenberg and Kohn[10] originally developed Density Functional theory for application to the ground state of a system of spinless fermions. In such a system the particle density is given by
with 
being the many-body ground state wavefunction of the
system. It can be shown that the total ground state energy of the
system is a functional of the density, 
, and that if
the energy due to the electron-ion interactions is excluded the
remainder of the energy is a universal functional of the density,
(i.e. does not depend on the
potential from the ions). The most elegant proof of Density
Functional theory is due to Levy[11] and is as
follows:
For a particular N-representable density
(i.e. any density given by an antisymmetric N-electron
wavefunction), a functional of the density corresponding to any
operator 
can be defined via
The right hand side is evaluated by searching over wavefunctions,
, which give rise to the density 
and looking for
the one which makes the expectation value of the operator a
minimum.
We can define in the same way, where
and
Now let be the ground state of an N-electron system and
a state which yields a density and minimises
.
Then, from the definition of ,
Now 
is the electronic Hamiltonian, from
Eq.(
), and so must obey the
variational principle (see section ),
Also, from the definition of , in Eq.(), we
have
since is just one of the trial wavefunctions
that yield 
. Adding 
to the above equation gives
which in combination with Eq.() yields the desired result
hence completing the proof.
