Kohn and Sham [9] introduced a method based on the
Hohenberg-Kohn theorem that enables one to minimise the functional
by varying 
over all densities
containing N electrons. This constraint is introduced by the Lagrange
multiplier, 
, chosen so that 
,
Kohn and Sham chose to separate 
into three parts,
so that becomes
where 
is defined as the kinetic energy
of a non-interacting electron gas with density ,
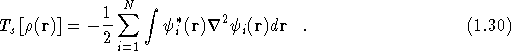
Eq.(
) also acts as a definition for the
exchange-correlation energy functional, 
. We
can now rewrite Eq.() in terms of an effective potential,
, as follows
where
and
Now, if one considers a system that really contained
non-interacting electrons moving in an external potential equal to
, as defined in Eq.(), then the same
analysis would lead to exactly the same Eq.(). Therefore,
to find the groundstate energy and density, 
and
all one has to do is solve the one-electron
equations
As the density is constructed according to
these equations (-) must be solved
self-consistently with Eq.().
The above derivation assumes that the exchange-correlation functional
is known. At present numerical exchange-correlation potentials have
only been determined for a few simple model systems, and so most
current density functional calculations use the Local Density
Approximation (LDA). The LDA approximates the XC functional
to a simple function of the density at any position, 
. The
value of this function is the XC energy per electron in a uniform
homogeneous electron gas of density 
. The LDA expression
for 
is
The LDA is remarkably accurate, but often fails when the electrons are strongly correlated, as in systems containing d and f orbital electrons.
