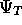The variational Quantum Monte Carlo method (VMC) was pioneered by
McMillan [1] to study liquid He and first applied to fermion
problems by Ceperly, Chester and Kalos [3]. The technique
is based on calculating a variational upper bound to the ground state
energy of the system. This is achieved by choosing a trial wavefunction,
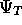based on knowledge of the physics of the system (see section
) and calculating the ground state energy according to
where the configuration R
represents the positions of all N electrons
in the system.
In a VMC calculation, () is rewritten in a form more
appropriate for Monte Carlo calculations. Define a new term, the
local energy as
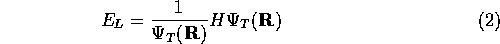
and introduce the multivariate probability distribution
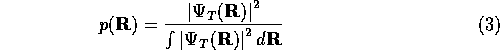
Note that p( R ) is always positive and normalised to 1. The variational energy can then be expressed as
where the Hamiltonian, H is
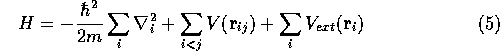
and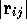 
is the separation between electron i and j and
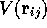is the Coulomb interaction.
The configurations, R
used in () are sampled from the
probability distribution,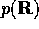 
by walking the configurations through
configuration space according to the Metropolis algorithm (see section
).
Having calculated an initial value for the energy using Eqn.(),
the trail wavefunction, 
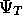can then be varied to try and improve on this
value by changing the values of any
variational parameters built into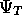 
.
