



Next: Optimising the support functions
Up: Density-matrices from Kohn-Sham orbitals
Previous: Projecting plane-wave eigenstates onto
Contents
In the case when the density-kernel 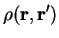 is expanded in terms of an
auxiliary matrix
is expanded in terms of an
auxiliary matrix 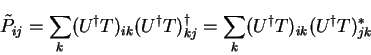 e.g. in order to construct a positive semi-definite
density-matrix, it is necessary to be able to calculate the auxiliary
matrix
e.g. in order to construct a positive semi-definite
density-matrix, it is necessary to be able to calculate the auxiliary
matrix 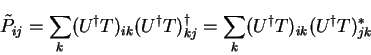 which corresponds to a given density-kernel
which corresponds to a given density-kernel 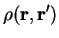 by
by
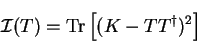 |
(8.14) |
This can be achieved by minimising the function 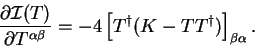 given by
given by
![\begin{displaymath}
{\cal I}(T) = {\rm Tr} \left[ (K - T T^{\dag })^2 \right]
\end{displaymath}](img1148.gif) |
(8.15) |
whose derivative with respect to 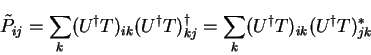 is
is
![\begin{displaymath}
\frac{\partial {\cal I}(T)}{\partial T^{\alpha \beta}} =
-4 \left[ T^{\dag } (K - T T^{\dag }) \right]_{\beta \alpha} .
\end{displaymath}](img1149.gif) |
(8.16) |
This derivative vanishes at the minimum, and so we find that the matrix
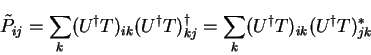 which minimises
which minimises 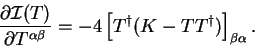 is the desired auxiliary matrix (the
solution
is the desired auxiliary matrix (the
solution 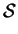 corresponds to a local maximum). We therefore choose to
minimise
corresponds to a local maximum). We therefore choose to
minimise  by the conjugate gradients method to obtain the
auxiliary matrix.
by the conjugate gradients method to obtain the
auxiliary matrix.




Next: Optimising the support functions
Up: Density-matrices from Kohn-Sham orbitals
Previous: Projecting plane-wave eigenstates onto
Contents
Peter D. Haynes
1999-09-21
![]() is expanded in terms of an
auxiliary matrix
is expanded in terms of an
auxiliary matrix ![]() e.g. in order to construct a positive semi-definite
density-matrix, it is necessary to be able to calculate the auxiliary
matrix
e.g. in order to construct a positive semi-definite
density-matrix, it is necessary to be able to calculate the auxiliary
matrix ![]() which corresponds to a given density-kernel
which corresponds to a given density-kernel ![]() by
by