



Next: Density-matrix initialisation
Up: Density-matrices from Kohn-Sham orbitals
Previous: Obtaining auxiliary matrices
Contents
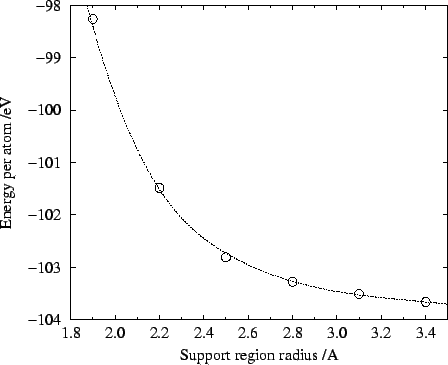
Optimising the support functions
As mentioned above, we can optimise our choice of support
functions by minimising the spilling parameter 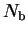 . We describe
this process here when the support functions are themselves described in
terms of a localised basis:
. We describe
this process here when the support functions are themselves described in
terms of a localised basis:
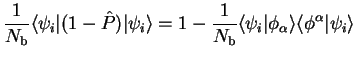 |
(8.17) |
The spilling parameter can be written in terms of the matrices 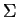 and
and 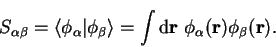 by:
by:
and we wish to obtain the gradients of 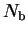 with respect to the
expansion coefficients
with respect to the
expansion coefficients
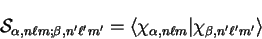 .
.
![\begin{displaymath}
\frac{\partial {\cal S}}{\partial c^{n \ell m}_{(\alpha)}} =...
...c{\partial L_{ki}}{\partial
c^{n \ell m}_{(\alpha)}} \right] .
\end{displaymath}](img1155.gif) |
(8.19) |
We obtain the derivative of the inverse matrix by differentiating
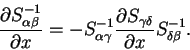 i.e.
i.e.
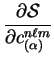 |
(8.20) |
which can be rearranged to give
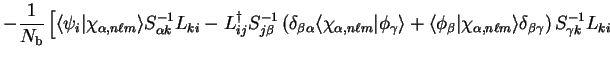 |
(8.21) |
Therefore (no summation over  )
)
In the case of the set of basis functions introduced in chapter 5,
the overlap between plane-wave eigenstates and localised basis functions,
e.g.
 , can be
calculated using the expression for the basis function Fourier transform
(5.9).
, can be
calculated using the expression for the basis function Fourier transform
(5.9).
We can use these gradients to minimise the spilling parameter (by the
conjugate gradients method) to obtain the set of optimal
coefficients
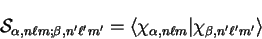 which define the set of
support functions which best span the space of the occupied plane-wave
orbitals.
The final minimum spilling parameter value also gives an estimate of the
quality of the basis-set being used.
which define the set of
support functions which best span the space of the occupied plane-wave
orbitals.
The final minimum spilling parameter value also gives an estimate of the
quality of the basis-set being used.




Next: Density-matrix initialisation
Up: Density-matrices from Kohn-Sham orbitals
Previous: Obtaining auxiliary matrices
Contents
Peter D. Haynes
1999-09-21
![]() . We describe
this process here when the support functions are themselves described in
terms of a localised basis:
. We describe
this process here when the support functions are themselves described in
terms of a localised basis:
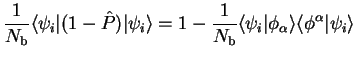
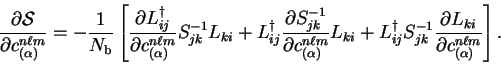
![$\displaystyle 1 - \frac{1}{N_{\mathrm b}} L_{i \alpha}^{\dag } S^{-1}_{\alpha \beta} L_{\beta i}
= 1 - \frac{1}{N_{\mathrm b}} {\rm Tr}[L^{\dag } S^{-1} L]$](img1154.gif)
![\begin{displaymath}
\frac{\partial {\cal S}}{\partial c^{n \ell m}_{(\alpha)}} =...
...c{\partial L_{ki}}{\partial
c^{n \ell m}_{(\alpha)}} \right] .
\end{displaymath}](img1155.gif)
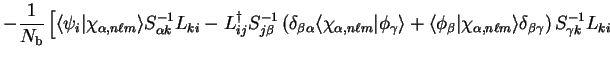
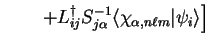
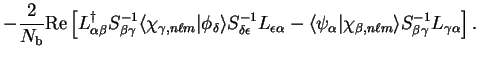
![$\displaystyle - \frac{2}{N_{\mathrm b}} {\rm Re} \left[ L_{\alpha \beta}^{\dag ...
...hi_{\beta , n \ell m} \rangle S_{\beta \gamma}^{-1}
L_{\gamma \alpha} \right] .$](img1162.gif)
![]() which define the set of
support functions which best span the space of the occupied plane-wave
orbitals.
The final minimum spilling parameter value also gives an estimate of the
quality of the basis-set being used.
which define the set of
support functions which best span the space of the occupied plane-wave
orbitals.
The final minimum spilling parameter value also gives an estimate of the
quality of the basis-set being used.