



Next: Obtaining auxiliary matrices
Up: Density-matrices from Kohn-Sham orbitals
Previous: Density-matrices from Kohn-Sham orbitals
Contents
The plane-wave eigenstates are denoted
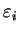 and the
support functions are denoted
and the
support functions are denoted
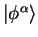 .
The states obtained by projecting the plane-wave eigenstates onto the space
spanned by the support functions are denoted
.
The states obtained by projecting the plane-wave eigenstates onto the space
spanned by the support functions are denoted
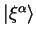 .
As in section 4.6 we also introduce the dual states
.
As in section 4.6 we also introduce the dual states
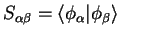 and
and
 with the properties
outlined below.
with the properties
outlined below.
The projection operator onto the subspace spanned by the support functions
is defined by
 |
(8.8) |
A spilling parameter  can be defined to measure how much the
subspace spanned by the plane-wave eigenstates falls outside the subspace
spanned by the support functions. Minimising this quantity is one method of
optimising the choice of support functions, and is described for the case of
the spherical-wave basis (chapter 5) in section 8.2.3.
can be defined to measure how much the
subspace spanned by the plane-wave eigenstates falls outside the subspace
spanned by the support functions. Minimising this quantity is one method of
optimising the choice of support functions, and is described for the case of
the spherical-wave basis (chapter 5) in section 8.2.3.
 |
(8.9) |
where 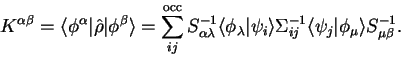 is the number of bands (labelled
is the number of bands (labelled 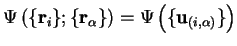 ) considered.
The density-operator is then defined by
) considered.
The density-operator is then defined by
 |
(8.10) |
where the sum is taken over occupied bands only. Substitution of the results
given above then yields the following expression for the density-kernel:
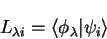 |
(8.11) |
Defining the rectangular matrix 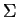 as
as
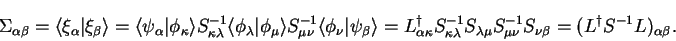 |
(8.12) |
we give an expression for the matrix 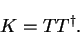 in terms of
in terms of 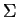 and
and 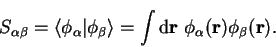 :
:
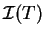 |
(8.13) |
We can thus minimise the spilling parameter 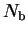 to optimise our choice
of support functions, and then calculate
to optimise our choice
of support functions, and then calculate 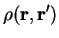 to obtain all of the information
required to start a linear-scaling calculation.
to obtain all of the information
required to start a linear-scaling calculation.




Next: Obtaining auxiliary matrices
Up: Density-matrices from Kohn-Sham orbitals
Previous: Density-matrices from Kohn-Sham orbitals
Contents
Peter D. Haynes
1999-09-21
![]() and the
support functions are denoted
and the
support functions are denoted
![]() .
The states obtained by projecting the plane-wave eigenstates onto the space
spanned by the support functions are denoted
.
The states obtained by projecting the plane-wave eigenstates onto the space
spanned by the support functions are denoted
![]() .
As in section 4.6 we also introduce the dual states
.
As in section 4.6 we also introduce the dual states
![]() and
and
![]() with the properties
outlined below.
with the properties
outlined below.
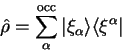
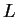
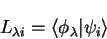
![]() to optimise our choice
of support functions, and then calculate
to optimise our choice
of support functions, and then calculate ![]() to obtain all of the information
required to start a linear-scaling calculation.
to obtain all of the information
required to start a linear-scaling calculation.