



Next: Implementation problems
Up: Kohn's method
Previous: Kohn's method
Contents
As mentioned in section 4.4.3, Kohn [135] has
suggested the use of a penalty functional to impose the idempotency
condition, and has proved a variational principle based upon it.
We consider trial density-matrices
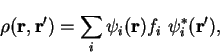 expressed in diagonal form with real orthonormal extended orbitals
expressed in diagonal form with real orthonormal extended orbitals
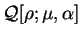 and occupation numbers
and occupation numbers
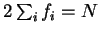 :
:
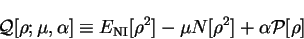 |
(6.1) |
The functional
![${\cal Q}[{\rho};\mu,\alpha]$](img797.gif) is then formed:
is then formed:
![\begin{displaymath}
{\cal Q}[{\rho};\mu,\alpha] \equiv E_{\mathrm{NI}}[{\rho}^2] -
\mu N[{\rho}^2] + \alpha {\cal P}[{\rho}]
\end{displaymath}](img798.gif) |
(6.2) |
in which
and where 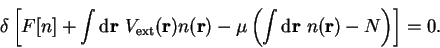 is the chemical potential and
is the chemical potential and  is a positive real
parameter.
is a positive real
parameter.
Kohn proves the following variational principle: that for some
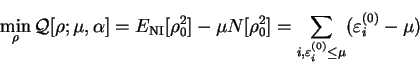 , the minimum value of
, the minimum value of
![${\cal Q}[{\rho};\mu,\alpha]$](img797.gif) is obtained for the idempotent ground-state
density-matrix
is obtained for the idempotent ground-state
density-matrix 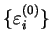 and that the minimum value is the ground-state grand potential i.e.
and that the minimum value is the ground-state grand potential i.e.
![\begin{displaymath}
\mathop{\rm min}\limits _{\rho} {\cal Q}[{\rho};\mu,\alpha] ...
...m_{i,\varepsilon^{(0)}_i \leq \mu} (\varepsilon^{(0)}_i - \mu)
\end{displaymath}](img808.gif) |
(6.6) |
in which the
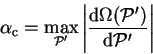 are the exact eigenvalues of the
self-consistent Hamiltonian, generated by the ground-state density-matrix
are the exact eigenvalues of the
self-consistent Hamiltonian, generated by the ground-state density-matrix
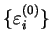 .
.
The critical value of  , denoted
, denoted
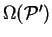 , is given by
, is given by
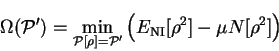 |
(6.7) |
in which
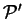 is the conditional minimum defined by
is the conditional minimum defined by
![\begin{displaymath}
\Omega({\cal P}') = \mathop{\rm min}\limits _{{\cal P}[{\rho...
...}'} \left( E_{\mathrm{NI}}[{\rho}^2]
- \mu N[{\rho}^2] \right)
\end{displaymath}](img813.gif) |
(6.8) |
i.e. the minimum grand potential for all trial density-matrices which give
a penalty functional value of 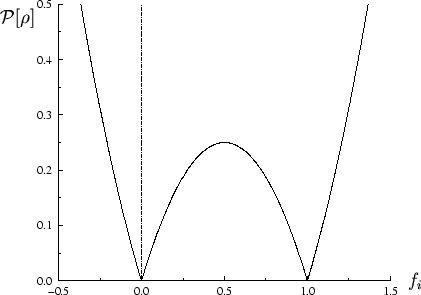 . Clearly
. Clearly
![\begin{displaymath}
\alpha_{\mathrm c} \geq \left\vert \frac{{\mathrm d} \Omega(...
..._i \leq \mu}
(\varepsilon^{(0)}_i - \mu)^2 \right]^{1 \over 2}
\end{displaymath}](img815.gif) |
(6.9) |
although this is only a lower bound on
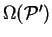 .
.
Kohn's variational principle is based on the non-interacting energy
![$E_{\mathrm{NI}}[\rho^2]$](img819.gif) . We now present a simple modification of this functional
based upon
self-consistent variation of the interacting energy. Consider the
functional
. We now present a simple modification of this functional
based upon
self-consistent variation of the interacting energy. Consider the
functional
![\begin{displaymath}
{\tilde {\cal Q}}[{\rho};\mu,\alpha] = E[{\rho}] - \mu N[{\rho}]
+ \alpha {\cal P}[{\rho}]
\end{displaymath}](img820.gif) |
(6.10) |
in which ![$E[{\rho}]$](img821.gif) is the interacting energy, and
is the interacting energy, and 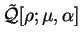 is
a positive semi-definite trial density-matrix. A given set of occupation
numbers
is
a positive semi-definite trial density-matrix. A given set of occupation
numbers 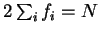 fixes the value of the penalty functional
fixes the value of the penalty functional
![${\cal P}[{\rho}]$](img823.gif) and variation
of
and variation
of
![${\tilde {\cal Q}}[{\rho};\mu,\alpha]$](img824.gif) with respect to the orbitals
with respect to the orbitals
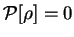 at fixed occupation numbers and subject to the
orthonormality constraint yields Kohn-Sham-like equations. Self-consistent
variation of the occupation numbers
at fixed occupation numbers and subject to the
orthonormality constraint yields Kohn-Sham-like equations. Self-consistent
variation of the occupation numbers 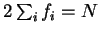 (i.e. allowing the
orbitals to relax, as in section 4.2) yields
(i.e. allowing the
orbitals to relax, as in section 4.2) yields
![\begin{displaymath}
\frac{\partial {\tilde {\cal Q}}[{\rho};\mu,\alpha]}{\partia...
... + \frac{\alpha}{{\cal P}[{\rho}]}
f_i (1 - f_i) (1 - 2 f_i) .
\end{displaymath}](img826.gif) |
(6.11) |
In the case of idempotent density-matrices,
for which
![${\cal P}[{\rho}]=0$](img827.gif) , we obtain the special cases
, we obtain the special cases
![\begin{displaymath}
\left.\frac{\partial {\tilde Q}[{\rho};\mu,\alpha]}
{\partia...
..._i=(0^{\pm},1^{\pm})} = 2 ({\varepsilon}_i - \mu)
\pm \alpha .
\end{displaymath}](img828.gif) |
(6.12) |
For this functional the critical value of  , again denoted
, again denoted
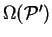 , is
given by
, is
given by
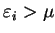 |
(6.13) |
where the maximum is strictly over those density-matrices searched during the
minimisation.
For
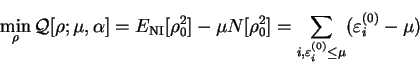 the total functional
the total functional
![${\tilde {\cal Q}}[{\rho};\mu,\alpha]$](img824.gif) takes its minimum value when
takes its minimum value when
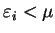 for
for
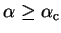 and
and
 respectively. In particular, for the
ground-state density-matrix
respectively. In particular, for the
ground-state density-matrix 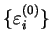 , the functional is strictly increasing
with respect to all variations in occupation numbers. The discontinuity in
the occupation number derivative of the penalty functional at idempotency is
required because of the non-variational behaviour of the total energy
with respect to these variations (section 4.2).
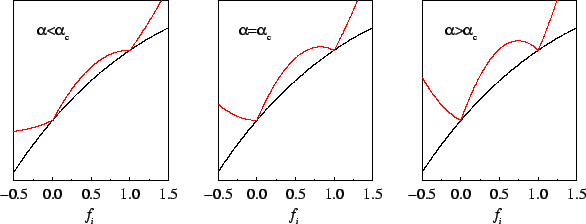
The behaviour of the penalty functional for unconstrained occupation
number variation is plotted in figure 6.1, and in figure
6.2 the total functional is sketched schematically for
several representative values of the parameter
, the functional is strictly increasing
with respect to all variations in occupation numbers. The discontinuity in
the occupation number derivative of the penalty functional at idempotency is
required because of the non-variational behaviour of the total energy
with respect to these variations (section 4.2).
The behaviour of the penalty functional for unconstrained occupation
number variation is plotted in figure 6.1, and in figure
6.2 the total functional is sketched schematically for
several representative values of the parameter  . This demonstrates
how the minimising density-matrix is idempotent only for
. This demonstrates
how the minimising density-matrix is idempotent only for
 .
.
Figure 6.2:
Schematic illustration of Kohn's variational principle: behaviour of the total energy (black) and total functional (red) for representative values of  .
.
|




Next: Implementation problems
Up: Kohn's method
Previous: Kohn's method
Contents
Peter D. Haynes
1999-09-21
![]() expressed in diagonal form with real orthonormal extended orbitals
expressed in diagonal form with real orthonormal extended orbitals
![]() and occupation numbers
and occupation numbers
![]() :
:
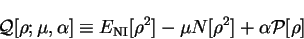
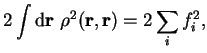
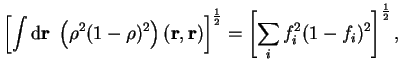
![$\displaystyle \left[ \int {\mathrm d}{\bf r}~ \left(
{\rho}^2(1 - {\rho})^2 \ri...
...r})
\right]^{1 \over 2} = \left[ \sum_i f_i^2
(1 - f_i)^2 \right]^{1 \over 2} ,$](img805.gif)
![]() , the minimum value of
, the minimum value of
![]() is obtained for the idempotent ground-state
density-matrix
is obtained for the idempotent ground-state
density-matrix ![]() and that the minimum value is the ground-state grand potential i.e.
and that the minimum value is the ground-state grand potential i.e. ![\begin{displaymath}
\mathop{\rm min}\limits _{\rho} {\cal Q}[{\rho};\mu,\alpha] ...
...m_{i,\varepsilon^{(0)}_i \leq \mu} (\varepsilon^{(0)}_i - \mu)
\end{displaymath}](img808.gif)
![]() , denoted
, denoted
![]() , is given by
, is given by
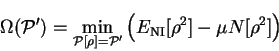
![\begin{displaymath}
\Omega({\cal P}') = \mathop{\rm min}\limits _{{\cal P}[{\rho...
...}'} \left( E_{\mathrm{NI}}[{\rho}^2]
- \mu N[{\rho}^2] \right)
\end{displaymath}](img813.gif)
![\begin{displaymath}
\alpha_{\mathrm c} \geq \left\vert \frac{{\mathrm d} \Omega(...
..._i \leq \mu}
(\varepsilon^{(0)}_i - \mu)^2 \right]^{1 \over 2}
\end{displaymath}](img815.gif)
![\begin{picture}(100,70)
\put(10,0){\includegraphics [width=8cm]{penfun.eps}}
\put(2,60){${\cal P}[\rho]$}
\put(92,2){$f_i$}
\end{picture}](img816.gif)
![]() . We now present a simple modification of this functional
based upon
self-consistent variation of the interacting energy. Consider the
functional
. We now present a simple modification of this functional
based upon
self-consistent variation of the interacting energy. Consider the
functional
![\begin{displaymath}
\frac{\partial {\tilde {\cal Q}}[{\rho};\mu,\alpha]}{\partia...
... + \frac{\alpha}{{\cal P}[{\rho}]}
f_i (1 - f_i) (1 - 2 f_i) .
\end{displaymath}](img826.gif)
![\begin{displaymath}
\left.\frac{\partial {\tilde Q}[{\rho};\mu,\alpha]}
{\partia...
..._i=(0^{\pm},1^{\pm})} = 2 ({\varepsilon}_i - \mu)
\pm \alpha .
\end{displaymath}](img828.gif)
![\includegraphics [width=13cm]{kohnfun.eps}](img834.gif)