



Next: 8.3 Density-matrix initialisation
Up: 8. Relating linear-scaling and
Previous: 8.1 Wave-functions from density-matrices
Contents
Subsections
8.2 Density-matrices from Kohn-Sham orbitals
This method is based upon work on the projection of plane-wave calculations
onto atomic orbitals [166], which has been used to
analyse atomic basis-sets [167] and obtain local atomic
properties from the extended Kohn-Sham orbitals [168].
Here we review the method, for the special case of a 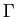 -point
Brillouin zone sampling.
-point
Brillouin zone sampling.
The plane-wave eigenstates are denoted
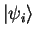 and the
support functions are denoted
and the
support functions are denoted
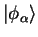 .
The states obtained by projecting the plane-wave eigenstates onto the space
spanned by the support functions are denoted
.
The states obtained by projecting the plane-wave eigenstates onto the space
spanned by the support functions are denoted
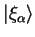 .
As in section 4.6 we also introduce the dual states
.
As in section 4.6 we also introduce the dual states
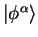 and
and
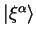 with the properties
outlined below.
with the properties
outlined below.
The projection operator onto the subspace spanned by the support functions
is defined by
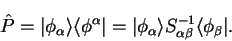 |
(8.8) |
A spilling parameter 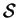 can be defined to measure how much the
subspace spanned by the plane-wave eigenstates falls outside the subspace
spanned by the support functions. Minimising this quantity is one method of
optimising the choice of support functions, and is described for the case of
the spherical-wave basis (chapter 5) in section 8.2.3.
can be defined to measure how much the
subspace spanned by the plane-wave eigenstates falls outside the subspace
spanned by the support functions. Minimising this quantity is one method of
optimising the choice of support functions, and is described for the case of
the spherical-wave basis (chapter 5) in section 8.2.3.
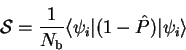 |
(8.9) |
where 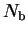 is the number of bands (labelled
is the number of bands (labelled 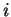 ) considered.
The density-operator is then defined by
) considered.
The density-operator is then defined by
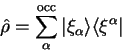 |
(8.10) |
where the sum is taken over occupied bands only. Substitution of the results
given above then yields the following expression for the density-kernel:
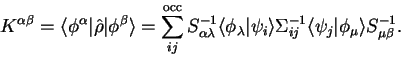 |
(8.11) |
Defining the rectangular matrix 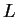 as
as
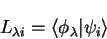 |
(8.12) |
we give an expression for the matrix 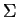 in terms of
in terms of 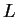 and
and 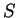 :
:
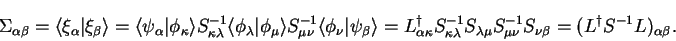 |
(8.13) |
We can thus minimise the spilling parameter 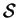 to optimise our choice
of support functions, and then calculate
to optimise our choice
of support functions, and then calculate 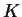 to obtain all of the information
required to start a linear-scaling calculation.
to obtain all of the information
required to start a linear-scaling calculation.
In the case when the density-kernel 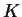 is expanded in terms of an
auxiliary matrix
is expanded in terms of an
auxiliary matrix 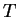 e.g. in order to construct a positive semi-definite
density-matrix, it is necessary to be able to calculate the auxiliary
matrix
e.g. in order to construct a positive semi-definite
density-matrix, it is necessary to be able to calculate the auxiliary
matrix 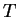 which corresponds to a given density-kernel
which corresponds to a given density-kernel 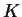 by
by
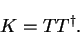 |
(8.14) |
This can be achieved by minimising the function 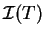 given by
given by
![\begin{displaymath}
{\cal I}(T) = {\rm Tr} \left[ (K - T T^{\dag })^2 \right]
\end{displaymath}](img1146.gif) |
(8.15) |
whose derivative with respect to 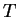 is
is
![\begin{displaymath}
\frac{\partial {\cal I}(T)}{\partial T^{\alpha \beta}} =
-4 \left[ T^{\dag } (K - T T^{\dag }) \right]_{\beta \alpha} .
\end{displaymath}](img1147.gif) |
(8.16) |
This derivative vanishes at the minimum, and so we find that the matrix
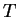 which minimises
which minimises 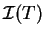 is the desired auxiliary matrix (the
solution
is the desired auxiliary matrix (the
solution 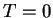 corresponds to a local maximum). We therefore choose to
minimise
corresponds to a local maximum). We therefore choose to
minimise 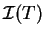 by the conjugate gradients method to obtain the
auxiliary matrix.
by the conjugate gradients method to obtain the
auxiliary matrix.
8.2.3 Optimising the support functions
As mentioned above, we can optimise our choice of support
functions by minimising the spilling parameter 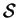 . We describe
this process here when the support functions are themselves described in
terms of a localised basis:
. We describe
this process here when the support functions are themselves described in
terms of a localised basis:
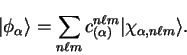 |
(8.17) |
The spilling parameter can be written in terms of the matrices 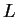 and
and 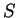 by:
by:
and we wish to obtain the gradients of 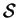 with respect to the
expansion coefficients
with respect to the
expansion coefficients
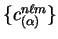 .
.
![\begin{displaymath}
\frac{\partial {\cal S}}{\partial c^{n \ell m}_{(\alpha)}} =...
...c{\partial L_{ki}}{\partial
c^{n \ell m}_{(\alpha)}} \right] .
\end{displaymath}](img1153.gif) |
(8.19) |
We obtain the derivative of the inverse matrix by differentiating
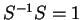 i.e.
i.e.
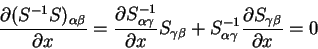 |
(8.20) |
which can be rearranged to give
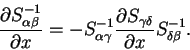 |
(8.21) |
Therefore (no summation over  )
)
In the case of the set of basis functions introduced in chapter 5,
the overlap between plane-wave eigenstates and localised basis functions,
e.g.
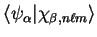 , can be
calculated using the expression for the basis function Fourier transform
(5.9).
, can be
calculated using the expression for the basis function Fourier transform
(5.9).
We can use these gradients to minimise the spilling parameter (by the
conjugate gradients method) to obtain the set of optimal
coefficients
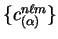 which define the set of
support functions which best span the space of the occupied plane-wave
orbitals.
The final minimum spilling parameter value also gives an estimate of the
quality of the basis-set being used.
which define the set of
support functions which best span the space of the occupied plane-wave
orbitals.
The final minimum spilling parameter value also gives an estimate of the
quality of the basis-set being used.




Next: 8.3 Density-matrix initialisation
Up: 8. Relating linear-scaling and
Previous: 8.1 Wave-functions from density-matrices
Contents
Peter Haynes
![]() -point
Brillouin zone sampling.
-point
Brillouin zone sampling.
![]() and the
support functions are denoted
and the
support functions are denoted
![]() .
The states obtained by projecting the plane-wave eigenstates onto the space
spanned by the support functions are denoted
.
The states obtained by projecting the plane-wave eigenstates onto the space
spanned by the support functions are denoted
![]() .
As in section 4.6 we also introduce the dual states
.
As in section 4.6 we also introduce the dual states
![]() and
and
![]() with the properties
outlined below.
with the properties
outlined below.
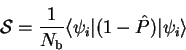
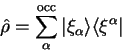
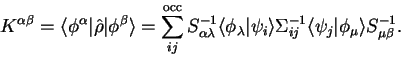
![]() to optimise our choice
of support functions, and then calculate
to optimise our choice
of support functions, and then calculate ![]() to obtain all of the information
required to start a linear-scaling calculation.
to obtain all of the information
required to start a linear-scaling calculation.
![]() is expanded in terms of an
auxiliary matrix
is expanded in terms of an
auxiliary matrix ![]() e.g. in order to construct a positive semi-definite
density-matrix, it is necessary to be able to calculate the auxiliary
matrix
e.g. in order to construct a positive semi-definite
density-matrix, it is necessary to be able to calculate the auxiliary
matrix ![]() which corresponds to a given density-kernel
which corresponds to a given density-kernel ![]() by
by
![]() . We describe
this process here when the support functions are themselves described in
terms of a localised basis:
. We describe
this process here when the support functions are themselves described in
terms of a localised basis:
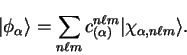
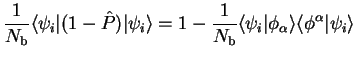
![$\displaystyle 1 - \frac{1}{N_{\mathrm b}} L_{i \alpha}^{\dag } S^{-1}_{\alpha \beta} L_{\beta i}
= 1 - \frac{1}{N_{\mathrm b}} {\rm Tr}[L^{\dag } S^{-1} L]$](img1152.gif)
![\begin{displaymath}
\frac{\partial {\cal S}}{\partial c^{n \ell m}_{(\alpha)}} =...
...c{\partial L_{ki}}{\partial
c^{n \ell m}_{(\alpha)}} \right] .
\end{displaymath}](img1153.gif)
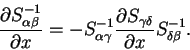
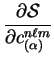
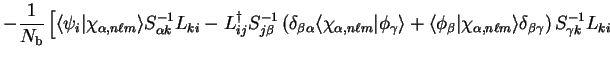
![$\displaystyle - \frac{2}{N_{\mathrm b}} {\rm Re} \left[ L_{\alpha \beta}^{\dag ...
...hi_{\beta , n \ell m} \rangle S_{\beta \gamma}^{-1}
L_{\gamma \alpha} \right] .$](img1160.gif)
![]() which define the set of
support functions which best span the space of the occupied plane-wave
orbitals.
The final minimum spilling parameter value also gives an estimate of the
quality of the basis-set being used.
which define the set of
support functions which best span the space of the occupied plane-wave
orbitals.
The final minimum spilling parameter value also gives an estimate of the
quality of the basis-set being used.