



Next: 8.2 Density-matrices from Kohn-Sham
Up: 8. Relating linear-scaling and
Previous: 8. Relating linear-scaling and
Contents
In the linear-scaling method, we have a density-matrix represented in the
form
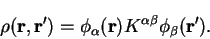 |
(8.1) |
First we represent the localised support functions by linear combinations of
plane-waves. For the analytic basis-set described in chapter 5
this is easily accomplished using equation 5.9 which gives
the Fourier transform of the basis functions.
Having obtained an expansion for the support functions in a complete
basis-set, it is now possible to orthogonalise the support functions
by means of the Löwdin transformation to the set of orthonormal orbitals
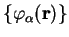 given by
given by
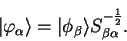 |
(8.2) |
Simultaneously transforming the matrix 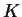 into the matrix
into the matrix 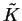 by
by
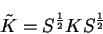 |
(8.3) |
leaves the density-matrix invariant in the sense that
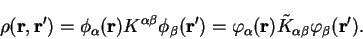 |
(8.4) |
To obtain the Kohn-Sham orbitals and occupation numbers it is necessary to
diagonalise 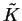 . If this density-matrix is a ground-state
density-matrix, then the density-operator and Hamiltonian commute so that
they have the same diagonal representation, and therefore diagonalising
. If this density-matrix is a ground-state
density-matrix, then the density-operator and Hamiltonian commute so that
they have the same diagonal representation, and therefore diagonalising 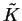 is equivalent to diagonalising
is equivalent to diagonalising
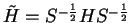 .
Thus the unitary transformation
.
Thus the unitary transformation 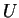 which yields the occupation numbers
which yields the occupation numbers
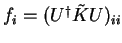 (no summation convention) also yields the
Kohn-Sham orbitals
(no summation convention) also yields the
Kohn-Sham orbitals
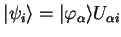 .
This information can then be used in a traditional plane-wave code, and this
is the method which was used to check the analytic results for the kinetic
energy and
non-local pseudopotential energy in chapter 5. The spatial
cut-off of the support regions in real-space leads to algebraically-decaying
oscillatory behaviour for large wave-vectors in reciprocal-space, so that a
single basis function needs a high plane-wave energy cut-off to accurately
describe this truncation.
However, for support functions which decay smoothly
to zero at the edge of the support region, the decay will be much faster, and
the plane-wave cut-off comparable to the cut-off for the basis
functions themselves.
.
This information can then be used in a traditional plane-wave code, and this
is the method which was used to check the analytic results for the kinetic
energy and
non-local pseudopotential energy in chapter 5. The spatial
cut-off of the support regions in real-space leads to algebraically-decaying
oscillatory behaviour for large wave-vectors in reciprocal-space, so that a
single basis function needs a high plane-wave energy cut-off to accurately
describe this truncation.
However, for support functions which decay smoothly
to zero at the edge of the support region, the decay will be much faster, and
the plane-wave cut-off comparable to the cut-off for the basis
functions themselves.




Next: 8.2 Density-matrices from Kohn-Sham
Up: 8. Relating linear-scaling and
Previous: 8. Relating linear-scaling and
Contents
Peter Haynes
![]() given by
given by
![]() . If this density-matrix is a ground-state
density-matrix, then the density-operator and Hamiltonian commute so that
they have the same diagonal representation, and therefore diagonalising
. If this density-matrix is a ground-state
density-matrix, then the density-operator and Hamiltonian commute so that
they have the same diagonal representation, and therefore diagonalising ![]() is equivalent to diagonalising
is equivalent to diagonalising
![]() .
Thus the unitary transformation
.
Thus the unitary transformation ![]() which yields the occupation numbers
which yields the occupation numbers
![]() (no summation convention) also yields the
Kohn-Sham orbitals
(no summation convention) also yields the
Kohn-Sham orbitals
![]() .
This information can then be used in a traditional plane-wave code, and this
is the method which was used to check the analytic results for the kinetic
energy and
non-local pseudopotential energy in chapter 5. The spatial
cut-off of the support regions in real-space leads to algebraically-decaying
oscillatory behaviour for large wave-vectors in reciprocal-space, so that a
single basis function needs a high plane-wave energy cut-off to accurately
describe this truncation.
However, for support functions which decay smoothly
to zero at the edge of the support region, the decay will be much faster, and
the plane-wave cut-off comparable to the cut-off for the basis
functions themselves.
.
This information can then be used in a traditional plane-wave code, and this
is the method which was used to check the analytic results for the kinetic
energy and
non-local pseudopotential energy in chapter 5. The spatial
cut-off of the support regions in real-space leads to algebraically-decaying
oscillatory behaviour for large wave-vectors in reciprocal-space, so that a
single basis function needs a high plane-wave energy cut-off to accurately
describe this truncation.
However, for support functions which decay smoothly
to zero at the edge of the support region, the decay will be much faster, and
the plane-wave cut-off comparable to the cut-off for the basis
functions themselves.