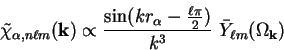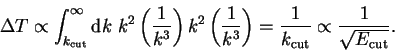Next: 5.6 Non-local pseudopotential
Up: 5. Localised basis-set
Previous: 5.4 Overlap matrix elements
Contents
The kinetic energy matrix elements for any two basis functions
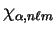 and
and
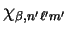 centred at
centred at
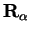 and
and
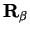 respectively are defined by
respectively are defined by
Because of the discontinuity in the first derivatives of the basis
functions at the sphere boundaries, a delta-function arises when the
Laplacian operates on a basis function. This is integrated out when
the matrix element is calculated and this contribution is included
when transforming the real-space integral to reciprocal-space in
equation 5.26.
The second line of equation 5.26 is identical to
equation 5.11 apart from a factor of
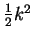 .
The same
separation into individually regular terms can be applied here, and
the result is that we need to calculate the contour integral
(5.17) as before, except that the integer
.
The same
separation into individually regular terms can be applied here, and
the result is that we need to calculate the contour integral
(5.17) as before, except that the integer 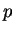 must be
replaced by
must be
replaced by 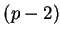 and a numerical factor of
and a numerical factor of
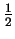 is
introduced. The calculation of the residues is identical to that
presented in the previous section, except that the integrand no longer
always has a pole at
is
introduced. The calculation of the residues is identical to that
presented in the previous section, except that the integrand no longer
always has a pole at 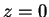 in every term.
in every term.
The results for
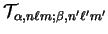 when
when
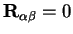 are
are
| |
|
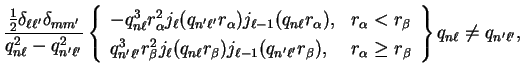 |
|
| |
|
|
(5.27) |
| |
|
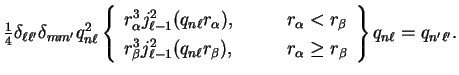 |
|
The calculation of the kinetic energy has been checked by
projecting a set of wave-functions expanded in the spherical-wave
basis onto the plane-wave basis using equation 5.9a. As
the kinetic energy cut-off for the plane-wave basis is increased, so
the description of the wave-functions becomes more accurate. The
kinetic energy calculated using the results above can then be compared
against the kinetic energy calculated by the plane-wave  CASTEP code [82].
CASTEP code [82].
From the asymptotic behaviour of the spherical Bessel functions,
the Fourier transform (5.9a) for large 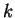 is
is
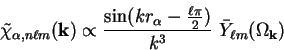 |
(5.28) |
and so the error in the kinetic energy due to truncating the
plane-wave basis with cut-off
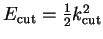 is
is
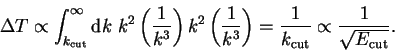 |
(5.29) |
In figure 5.1 the kinetic energy as calculated by the
plane-wave code has been plotted against
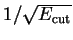 and yields a straight line as expected, which can then be extrapolated
to obtain an estimate of the kinetic energy calculated for infinite
cut-off:
and yields a straight line as expected, which can then be extrapolated
to obtain an estimate of the kinetic energy calculated for infinite
cut-off:
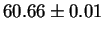 eV. This is in agreement with the value
calculated analytically of
eV. This is in agreement with the value
calculated analytically of 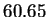 eV.
eV.
Figure 5.1:
Plot of asymptotic fit to kinetic energy data.
|
|




Next: 5.6 Non-local pseudopotential
Up: 5. Localised basis-set
Previous: 5.4 Overlap matrix elements
Contents
Peter Haynes
![]() and
and
![]() centred at
centred at
![]() and
and
![]() respectively are defined by
respectively are defined by
![]() .
The same
separation into individually regular terms can be applied here, and
the result is that we need to calculate the contour integral
(5.17) as before, except that the integer
.
The same
separation into individually regular terms can be applied here, and
the result is that we need to calculate the contour integral
(5.17) as before, except that the integer ![]() must be
replaced by
must be
replaced by ![]() and a numerical factor of
and a numerical factor of
![]() is
introduced. The calculation of the residues is identical to that
presented in the previous section, except that the integrand no longer
always has a pole at
is
introduced. The calculation of the residues is identical to that
presented in the previous section, except that the integrand no longer
always has a pole at ![]() in every term.
in every term.
![]() when
when
![]() are
are
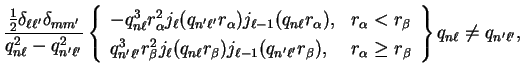
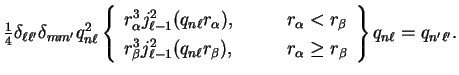
![]() is
is