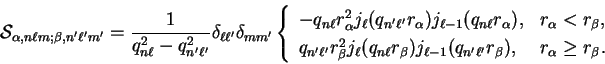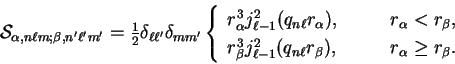Next: 5.5 Kinetic energy matrix
Up: 5. Localised basis-set
Previous: 5.3 Fourier transform of
Contents
5.4 Overlap matrix elements
The overlap matrix for any two basis functions
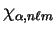 and
and
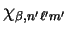 centred at
centred at
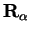 and
and
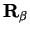 respectively is
respectively is
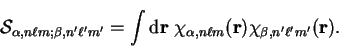 |
(5.10) |
Defining
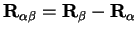 , and using the result for the Fourier transform of the basis
functions, the integral can be rewritten as
, and using the result for the Fourier transform of the basis
functions, the integral can be rewritten as
 |
(5.11) |
Using equation 5.9a we obtain
 |
(5.12) |
where
 is the integral
is the integral
 |
(5.13) |
Introducing differential operators
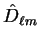 , obtained from
, obtained from
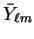 by making the replacement
by making the replacement
where
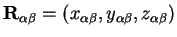 in Cartesian coordinates, equation
5.13 becomes
in Cartesian coordinates, equation
5.13 becomes
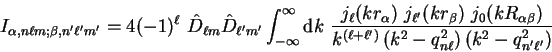 |
(5.14) |
where we have used the fact that the integrand is an even function of
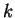 for all values of
for all values of 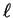 and
and 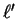 to change the limits of the
integral. From equation 5.14
to change the limits of the
integral. From equation 5.14
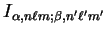 no longer
appears manifestly symmetric with respect to swapping
no longer
appears manifestly symmetric with respect to swapping  and
and
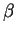 (since there is no
(since there is no 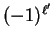 term).
Nonetheless, it still is because under the swap
term).
Nonetheless, it still is because under the swap
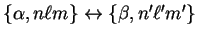 ,
,
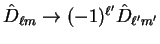 and
and
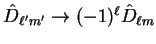 .
.
The three spherical Bessel functions in equation 5.14
can all be expressed in terms of trigonometric functions and algebraic
powers of the argument, using the recursion rules
(A.1, A.2). The product of three
trigonometric functions can always be expressed as a sum of four
trigonometric functions with different arguments, using well-known
identities. The result is to split the integrand up into terms of the
following form:
These terms are individually singular and generally possess a pole of
order 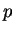 on the real axis at
on the real axis at 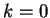 and cannot be
integrated. However, since we are integrating finite well-behaved
functions over a finite volume of space, we know that the total integrand cannot contain any
non-integrable singularities. Therefore we can add extra contributions
to each term to cancel all the singularities except simple poles, in the knowledge that
all these extra terms must cancel when the terms are added together to
obtain the total integrand.
and cannot be
integrated. However, since we are integrating finite well-behaved
functions over a finite volume of space, we know that the total integrand cannot contain any
non-integrable singularities. Therefore we can add extra contributions
to each term to cancel all the singularities except simple poles, in the knowledge that
all these extra terms must cancel when the terms are added together to
obtain the total integrand.
We shall evaluate the integrals using the calculus of residues so
that the general integral to be performed is
![\begin{displaymath}
I = \oint_C {\mathrm d}z ~ \frac{\exp[{\mathrm{i}} R z]}{z^p...
...^2 - q_{n
\ell}^2 \right) \left( z^2 - q_{n' \ell'}^2 \right)}
\end{displaymath}](img669.gif) |
(5.16) |
where
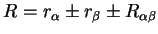 and the
contour
and the
contour 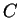 runs along the real
runs along the real 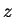 -axis from
-axis from 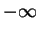 to
to 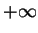 ,
and is closed in either the upper or lower half
,
and is closed in either the upper or lower half 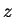 -plane, depending
upon whether
-plane, depending
upon whether 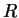 is positive or negative respectively. Adding the
extra terms to remove the non-integrable singularities we obtain the final form of the
integral
is positive or negative respectively. Adding the
extra terms to remove the non-integrable singularities we obtain the final form of the
integral
![\begin{displaymath}
I = \oint_C {\mathrm d}z ~ \frac{\exp[{\mathrm{i}} R z] - \s...
... - q_{n \ell}^2 \right)
\left( z^2 - q_{n' \ell'}^2 \right)} .
\end{displaymath}](img675.gif) |
(5.17) |
This integrand has simple poles lying on the contour of
integration at
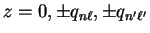 . The residues
of these poles are
. The residues
of these poles are
Summing the residues to perform the Cauchy principal value integrals,
and taking real or imaginary parts as appropriate, we obtain the
following results:
where
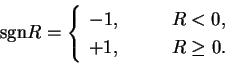 |
(5.21) |
For the case when
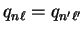 , we note that since the
integrand in equation 5.17 must still only have a simple
pole at
, we note that since the
integrand in equation 5.17 must still only have a simple
pole at
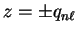 we obtain a simplified form in this
special case by taking the limit
we obtain a simplified form in this
special case by taking the limit
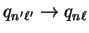 of equations 5.19 and 5.20.
of equations 5.19 and 5.20.
The result for
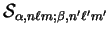 is obtained by summing the results
in equations
5.19, 5.20, 5.22 and
5.23 for all the terms in the expansion of the
integrand (5.14) and then operating with the differential
operators
is obtained by summing the results
in equations
5.19, 5.20, 5.22 and
5.23 for all the terms in the expansion of the
integrand (5.14) and then operating with the differential
operators
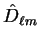 .
.
A second special case occurs when
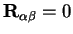 ,
and in this case it is simplest to perform the integral
(5.10) in real-space using the generalised orthogonality
relation for spherical Bessel functions (A.4) when
,
and in this case it is simplest to perform the integral
(5.10) in real-space using the generalised orthogonality
relation for spherical Bessel functions (A.4) when
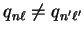 .
.
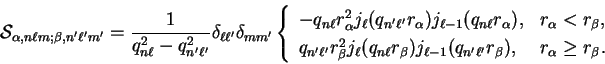 |
(5.24) |
There is also the case when
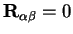 and
and
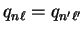 which is calculated using equation
A.5.
which is calculated using equation
A.5.
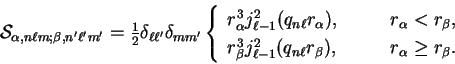 |
(5.25) |
Finally, it is obvious that the overlap matrix element must vanish
when the separation of the the sphere centres exceeds the sum of their
radii (i.e.
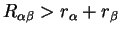 ) because then
there is no region of space where both basis functions are
non-zero. However, this is not obvious from the results presented
above, but arises because of the change of sign of the residue sums in
equations
5.19, 5.20, 5.22 and
5.23 (denoted by
) because then
there is no region of space where both basis functions are
non-zero. However, this is not obvious from the results presented
above, but arises because of the change of sign of the residue sums in
equations
5.19, 5.20, 5.22 and
5.23 (denoted by
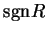 ) which occurs when
) which occurs when
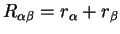 and results in the exact
cancellation of all terms.
and results in the exact
cancellation of all terms.




Next: 5.5 Kinetic energy matrix
Up: 5. Localised basis-set
Previous: 5.3 Fourier transform of
Contents
Peter Haynes
![]() and
and
![]() centred at
centred at
![]() and
and
![]() respectively is
respectively is
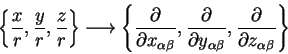
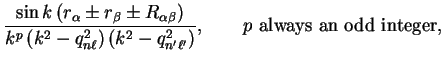
![\begin{displaymath}
I = \oint_C {\mathrm d}z ~ \frac{\exp[{\mathrm{i}} R z]}{z^p...
...^2 - q_{n
\ell}^2 \right) \left( z^2 - q_{n' \ell'}^2 \right)}
\end{displaymath}](img669.gif)
![$\displaystyle \frac{\exp[\pm {\mathrm{i}} q_{n
\ell} R] - \sum_{m=0}^{p-2} {(\p...
...n \ell}^2 - q_{n' \ell'}^2 \right) \left( \pm q_{n
\ell} \right)^{p+1}}, \qquad$](img679.gif)
![]() ,
and in this case it is simplest to perform the integral
(5.10) in real-space using the generalised orthogonality
relation for spherical Bessel functions (A.4) when
,
and in this case it is simplest to perform the integral
(5.10) in real-space using the generalised orthogonality
relation for spherical Bessel functions (A.4) when
![]() .
.