As described in section 3.3, in the pseudopotential approximation, the core electrons and strong ionic potential of the atom are replaced by a much weaker potential in which the remaining pseudo-valence electrons move. The pseudo-valence states no longer have to be orthogonal to lower-lying core states and hence are much smoother than the all-electron valence states in the core region and have less kinetic energy. Thus the pseudo-valence states can be accurately represented by a much smaller set of plane-wave basis functions than the all-electron states.
The plane-wave basis state
![]() is a solution of the Helmholtz equation (the time-independent
free-electron Schrödinger equation)
is a solution of the Helmholtz equation (the time-independent
free-electron Schrödinger equation)
If instead we wish to localise the basis functions, say within
spherical regions of radius ![]() , so that the function vanishes outside
these regions, then appropriate conditions would be to require the
functions to be finite within the regions and to vanish on the
boundary. The solutions to the Helmholtz equation 5.1
subject to these conditions are then truncated spherical-waves
, so that the function vanishes outside
these regions, then appropriate conditions would be to require the
functions to be finite within the regions and to vanish on the
boundary. The solutions to the Helmholtz equation 5.1
subject to these conditions are then truncated spherical-waves
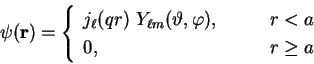 |
(5.2) |
We note that these functions solve the same equation as the
plane-wave basis functions, so that within the pseudopotential
approximation the wave-functions will be well-described by a truncated
set of these basis functions. Moreover, these functions are
eigenstates of the kinetic energy operator within the localisation
region ![]() (i.e. in the region in which they will be used to
describe the wave-functions) with eigenvalue
(i.e. in the region in which they will be used to
describe the wave-functions) with eigenvalue
![]() so
that the same kinetic energy cut-off used to truncate the plane-wave
basis can be used here to restrict the values of
so
that the same kinetic energy cut-off used to truncate the plane-wave
basis can be used here to restrict the values of ![]() and
and ![]() .
.
Since the Laplacian is a self-adjoint operator under these boundary conditions, application of Sturm-Liouville theory proves that all states within the same spherical region are mutually orthogonal.
In a calculation, the electronic states are described by covering
the simulation cell with overlapping spheres (known as support regions),
usually chosen to be
centred on the ions or bond-centres at positions
![]() , and expanding the
localised support functions
, and expanding the
localised support functions
![]() within these spheres in this basis:
within these spheres in this basis:
The expansion (5.3) is frequently written down formally, but rarely used computationally because of the inconvenience of using spherical Bessel functions in numerical work. However, the analytic results derived in the following sections offset this disadvantage.
As mentioned in section 3.2.2,
linear-scaling methods are aimed at large systems, and so the Brillouin
zone sampling of the electronic states is usually restricted to the
states at the ![]() -point only. The wave-functions can then be made
real without loss of generality, and so in practice we use real linear
combinations of the spherical harmonics defined below, which does not
alter any of the analysis here.
-point only. The wave-functions can then be made
real without loss of generality, and so in practice we use real linear
combinations of the spherical harmonics defined below, which does not
alter any of the analysis here.
![\begin{displaymath}
\{Y_{\ell m}\} \rightarrow \left\{
\begin{array}{rcl}
{\bar ...
...^m Y_{\ell,\vert m\vert} (\Omega) \right]
\end{array} \right\}
\end{displaymath}](img626.gif) |
(5.4) |
We introduce
![]() to represent a
truncated spherical-wave basis function centred at
to represent a
truncated spherical-wave basis function centred at
![]() and
confined to a sphere of radius
and
confined to a sphere of radius ![]() :
:
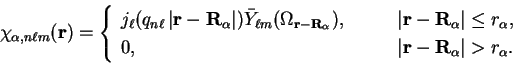 |
(5.5) |
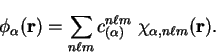 |
(5.6) |