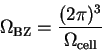Next: 3.3 The pseudopotential approximation
Up: 3. Quantum Mechanics of
Previous: 3.1 Density-functional theory
Contents
Subsections
3.2 Periodic systems
Exploiting the results of the previous section, we can now consider the
motion of non-interacting particles in a static potential, which is described
by the time-independent Schrödinger equation 3.20.
In the study of bulk crystals, the system is infinite but periodic, and so
it is necessary to be able to reduce this problem to the study of a finite
system. This approach turns out to have several advantages so that it is
often easiest to study even aperiodic systems by imposing some false
periodicity. The system is contained within a supercell which is then
replicated periodically throughout space (see figure 3.1).
The supercell must be large enough so that the systems contained within each
one, which in reality are isolated, do not interact significantly.
Figure 3.1:
Using the supercell approximation, an isolated molecule can be studied using the same techniques which
are usually applied to crystals.
|
|
3.2.1 Bloch's theorem
See [45] for a fuller discussion of the proof outlined here.
We consider non-interacting particles moving in a static potential 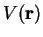 ,
which may be the Kohn-Sham effective potential
,
which may be the Kohn-Sham effective potential
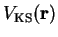 (3.18).
In a perfect crystal, the nuclei are arranged in a regular periodic array
described by a set of Bravais lattice vectors
(3.18).
In a perfect crystal, the nuclei are arranged in a regular periodic array
described by a set of Bravais lattice vectors 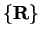 . The system,
being infinite, is invariant under translation by any of these lattice
vectors, and in particular the potential is also periodic i.e.
. The system,
being infinite, is invariant under translation by any of these lattice
vectors, and in particular the potential is also periodic i.e.
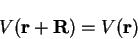 |
(3.31) |
for all Bravais lattice vectors 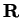 .
.
The Schrödinger equation which describes the motion of a single particle
in this potential is
![\begin{displaymath}
{\hat H} \vert \psi \rangle = \left[ -{\textstyle{1 \over 2}...
...})
\right] \vert \psi \rangle = \varepsilon \vert \psi \rangle
\end{displaymath}](img254.gif) |
(3.32) |
and we define translation operators
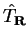 for each lattice vector
for each lattice vector
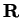 which act in the
following manner on any function of position
which act in the
following manner on any function of position 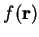 :
:
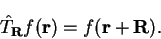 |
(3.33) |
Since the potential and hence the Hamiltonian are periodic i.e.
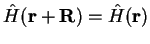 , these operators
commute with the translation operators:
, these operators
commute with the translation operators:
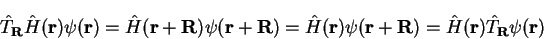 |
(3.34) |
i.e.
![$\left[ {\hat H} , {\hat T}_{\bf R} \right] = 0$](img260.gif) , and the translation
operators commute with each other i.e.
, and the translation
operators commute with each other i.e.
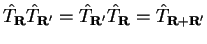 .
.
There must, therefore, exist a good quantum number corresponding to each
lattice vector 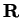 , and it must also be possible to choose the
eigenstates of the Hamiltonian to be simultaneous eigenstates of all the
translation operators;
, and it must also be possible to choose the
eigenstates of the Hamiltonian to be simultaneous eigenstates of all the
translation operators;
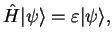 |
|
|
(3.35) |
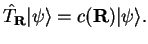 |
|
|
(3.36) |
From the commutation relations of the translation vectors it follows that
the eigenvalues must satisfy
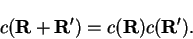 |
(3.37) |
We can define the eigenvalues for the three primitive lattice vectors
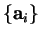 in terms of three complex numbers
in terms of three complex numbers 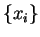 by
by
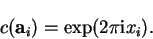 |
(3.38) |
Since all lattice vectors can be expressed in the form
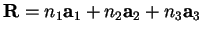 , where the
, where the 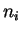 are integers,
it follows from equation
3.37 that
are integers,
it follows from equation
3.37 that
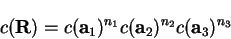 |
(3.39) |
which is equivalent to
where the
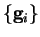 are the reciprocal lattice vectors satisfying
are the reciprocal lattice vectors satisfying
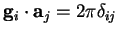 , and the
, and the 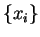 are
complex numbers in general.
are
complex numbers in general.
Thus we have shown that
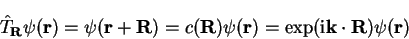 |
(3.42) |
which is one statement of Bloch's theorem. Consider the function
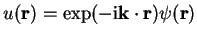 .
.
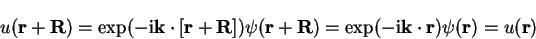 |
(3.43) |
i.e. the function 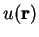 also has the periodicity of the lattice, and
so the wave-function
also has the periodicity of the lattice, and
so the wave-function 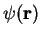 can also be expressed as
can also be expressed as
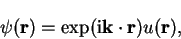 |
(3.44) |
where 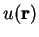 is a strictly cell-periodic function i.e.
is a strictly cell-periodic function i.e.
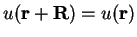 .
.
We thus label the eigenstates of the Hamiltonian and the translation operators
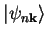 where
where 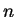 is the good quantum number labelling
different eigenstates of the Hamiltonian with the same good quantum vector
is the good quantum number labelling
different eigenstates of the Hamiltonian with the same good quantum vector
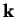 , related to the translational symmetry.
, related to the translational symmetry.
At this point we note that a periodic function can always be expressed
as a Fourier series i.e.
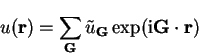 |
(3.45) |
where 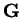 is reciprocal lattice vector
is reciprocal lattice vector
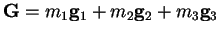 and the
and the 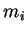 are integers.
Thus the state
are integers.
Thus the state
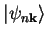 can be expressed as a linear
combination of plane-waves:
can be expressed as a linear
combination of plane-waves:
Instead of having to solve for a wave-function over all of (infinite)
space, the problem now becomes one of solving for wave-functions only
within a single (super)cell, albeit with an infinite number of possible values
for
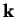 . In order to simplify the problem to manageable proportions, it is
necessary to impose some boundary conditions on the wave-function, which
restrict the allowed values of
. In order to simplify the problem to manageable proportions, it is
necessary to impose some boundary conditions on the wave-function, which
restrict the allowed values of 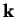 .
.
3.2.2 Brillouin zone sampling
We choose to model the infinite periodic system by a large number of primitive
cells
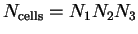 stacked together, with
stacked together, with 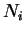 cells
along the
cells
along the 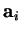 direction, and we apply periodic or generalised
Born-von Karman boundary conditions to the wave-functions, which can be
interpreted by saying that a particle which leaves one surface of the
crystal simultaneously enters the crystal at the opposite surface. In
fact it can be shown [46] that the choice of boundary
conditions does not affect the bulk properties of the system. This
condition is expressed mathematically as
direction, and we apply periodic or generalised
Born-von Karman boundary conditions to the wave-functions, which can be
interpreted by saying that a particle which leaves one surface of the
crystal simultaneously enters the crystal at the opposite surface. In
fact it can be shown [46] that the choice of boundary
conditions does not affect the bulk properties of the system. This
condition is expressed mathematically as
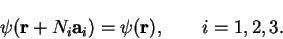 |
(3.48) |
Applying Bloch's theorem (3.42) gives
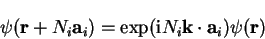 |
(3.49) |
so that the values of 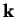 are restricted such that
are restricted such that
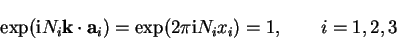 |
(3.50) |
using equation 3.41.
Therefore the values of the 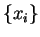 are required to be real and equal to
are required to be real and equal to
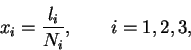 |
(3.51) |
where the 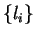 are integers, so that the general allowed form for
the Bloch wave-vectors
are integers, so that the general allowed form for
the Bloch wave-vectors 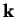 is
is
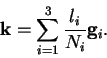 |
(3.52) |
Taking the limit to the true infinite perfect crystal (
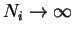 )
we see that there is still an infinite number of allowed
)
we see that there is still an infinite number of allowed 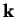 -vectors,
but that they are now members of a countably infinite set.
Furthermore, we see that
-vectors,
but that they are now members of a countably infinite set.
Furthermore, we see that 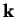 -vectors which differ only by a reciprocal
lattice vector are in fact equivalent. Consider two such wave-vectors related by
-vectors which differ only by a reciprocal
lattice vector are in fact equivalent. Consider two such wave-vectors related by
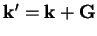 , then the corresponding Bloch states are also
related by
, then the corresponding Bloch states are also
related by
Since the expression in square brackets on the first line is a cell-periodic
function the whole expression is a valid Bloch wave-function with
wave-vector 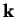 . Thus we can restrict our attention to those
. Thus we can restrict our attention to those
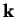 -vectors which lie within the first Brillouin zone, that
volume of reciprocal-space enclosing the origin which is bounded by the planes which
perpendicularly bisect lines from the origin to surrounding lattice points.
-vectors which lie within the first Brillouin zone, that
volume of reciprocal-space enclosing the origin which is bounded by the planes which
perpendicularly bisect lines from the origin to surrounding lattice points.
The situation now is that for each allowed 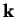 -vector within the first
Brillouin zone we must calculate the occupied Hamiltonian eigenstates in
order to construct the density. However, the wave-functions and other
properties such as Hamiltonian eigenvalues vary smoothly over the
Brillouin zone [47] so that in practice only a finite set
of points need to be chosen, and methods for making efficient choices have
been developed [48,49,50,51,52,53]. From the calculation of the wave-functions
at a certain set of
-vector within the first
Brillouin zone we must calculate the occupied Hamiltonian eigenstates in
order to construct the density. However, the wave-functions and other
properties such as Hamiltonian eigenvalues vary smoothly over the
Brillouin zone [47] so that in practice only a finite set
of points need to be chosen, and methods for making efficient choices have
been developed [48,49,50,51,52,53]. From the calculation of the wave-functions
at a certain set of 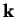 -points,
-points,
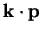 perturbation theory [54,55] can be used
to approximate the wave-functions at other nearby
perturbation theory [54,55] can be used
to approximate the wave-functions at other nearby 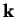 -points.
-points.
In this work, we are interested in the behaviour of very large systems. The
volume of the Brillouin zone
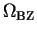 is related to the
volume of the supercell
is related to the
volume of the supercell
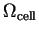 by
by
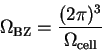 |
(3.54) |
so that for large systems, the Brillouin zone volume is very small and only
a few 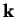 -points need to be considered to describe the variation
across the Brillouin zone accurately. In this work we therefore only
calculate the wave-functions at the centre of the Brillouin zone,
-points need to be considered to describe the variation
across the Brillouin zone accurately. In this work we therefore only
calculate the wave-functions at the centre of the Brillouin zone, 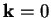 ,
known as the
,
known as the 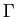 -point. This has the added advantage that at this
-point. This has the added advantage that at this
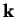 -point the wave-functions can be chosen to be real (recall that there
is always an arbitrary global phase factor) without loss of generality.
-point the wave-functions can be chosen to be real (recall that there
is always an arbitrary global phase factor) without loss of generality.




Next: 3.3 The pseudopotential approximation
Up: 3. Quantum Mechanics of
Previous: 3.1 Density-functional theory
Contents
Peter Haynes
![\includegraphics [height=7cm]{supercell.eps}](img250.gif)
![\includegraphics [height=7cm]{supercell.eps}](img250.gif)
![]() ,
which may be the Kohn-Sham effective potential
,
which may be the Kohn-Sham effective potential
![]() (3.18).
In a perfect crystal, the nuclei are arranged in a regular periodic array
described by a set of Bravais lattice vectors
(3.18).
In a perfect crystal, the nuclei are arranged in a regular periodic array
described by a set of Bravais lattice vectors ![]() . The system,
being infinite, is invariant under translation by any of these lattice
vectors, and in particular the potential is also periodic i.e.
. The system,
being infinite, is invariant under translation by any of these lattice
vectors, and in particular the potential is also periodic i.e. ![]() , these operators
commute with the translation operators:
, these operators
commute with the translation operators:
![]() , and it must also be possible to choose the
eigenstates of the Hamiltonian to be simultaneous eigenstates of all the
translation operators;
, and it must also be possible to choose the
eigenstates of the Hamiltonian to be simultaneous eigenstates of all the
translation operators;
![]() where
where ![]() is the good quantum number labelling
different eigenstates of the Hamiltonian with the same good quantum vector
is the good quantum number labelling
different eigenstates of the Hamiltonian with the same good quantum vector
![]() , related to the translational symmetry.
, related to the translational symmetry.
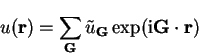
![]() . In order to simplify the problem to manageable proportions, it is
necessary to impose some boundary conditions on the wave-function, which
restrict the allowed values of
. In order to simplify the problem to manageable proportions, it is
necessary to impose some boundary conditions on the wave-function, which
restrict the allowed values of ![]() .
.
![]() stacked together, with
stacked together, with ![]() cells
along the
cells
along the ![]() direction, and we apply periodic or generalised
Born-von Karman boundary conditions to the wave-functions, which can be
interpreted by saying that a particle which leaves one surface of the
crystal simultaneously enters the crystal at the opposite surface. In
fact it can be shown [46] that the choice of boundary
conditions does not affect the bulk properties of the system. This
condition is expressed mathematically as
direction, and we apply periodic or generalised
Born-von Karman boundary conditions to the wave-functions, which can be
interpreted by saying that a particle which leaves one surface of the
crystal simultaneously enters the crystal at the opposite surface. In
fact it can be shown [46] that the choice of boundary
conditions does not affect the bulk properties of the system. This
condition is expressed mathematically as
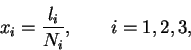
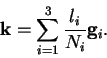
![]() )
we see that there is still an infinite number of allowed
)
we see that there is still an infinite number of allowed ![]() -vectors,
but that they are now members of a countably infinite set.
Furthermore, we see that
-vectors,
but that they are now members of a countably infinite set.
Furthermore, we see that ![]() -vectors which differ only by a reciprocal
lattice vector are in fact equivalent. Consider two such wave-vectors related by
-vectors which differ only by a reciprocal
lattice vector are in fact equivalent. Consider two such wave-vectors related by
![]() , then the corresponding Bloch states are also
related by
, then the corresponding Bloch states are also
related by
![]() -vector within the first
Brillouin zone we must calculate the occupied Hamiltonian eigenstates in
order to construct the density. However, the wave-functions and other
properties such as Hamiltonian eigenvalues vary smoothly over the
Brillouin zone [47] so that in practice only a finite set
of points need to be chosen, and methods for making efficient choices have
been developed [48,49,50,51,52,53]. From the calculation of the wave-functions
at a certain set of
-vector within the first
Brillouin zone we must calculate the occupied Hamiltonian eigenstates in
order to construct the density. However, the wave-functions and other
properties such as Hamiltonian eigenvalues vary smoothly over the
Brillouin zone [47] so that in practice only a finite set
of points need to be chosen, and methods for making efficient choices have
been developed [48,49,50,51,52,53]. From the calculation of the wave-functions
at a certain set of ![]() -points,
-points,
![]() perturbation theory [54,55] can be used
to approximate the wave-functions at other nearby
perturbation theory [54,55] can be used
to approximate the wave-functions at other nearby ![]() -points.
-points.
![]() is related to the
volume of the supercell
is related to the
volume of the supercell
![]() by
by