



Next: 3.2 Periodic systems
Up: 3. Quantum Mechanics of
Previous: 3. Quantum Mechanics of
Contents
Subsections
3.1 Density-functional theory
In this section we will describe the remarkable theorems of density-functional
theory (DFT) which allow us to find ground-state properties of a system
without dealing directly with the many-electron state
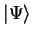 . We
deal with a system of
. We
deal with a system of 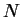 electrons moving in a static potential, and adopt
a conventional normalisation in which
electrons moving in a static potential, and adopt
a conventional normalisation in which
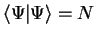 .
.
As a result of the Born-Oppenheimer approximation, the Coulomb potential
arising from the nuclei is treated as a static external potential
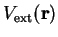 :
:
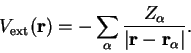 |
(3.1) |
We define the remainder of the electronic Hamiltonian given in
(2.19) as 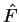 :
:
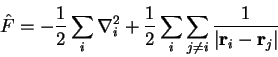 |
(3.2) |
such that
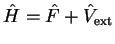 where
where
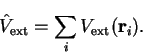 |
(3.3) |
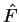 is the
same for all
is the
same for all 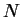 -electron systems, so that the Hamiltonian, and hence the
ground-state
-electron systems, so that the Hamiltonian, and hence the
ground-state
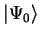 , are completely determined by
, are completely determined by 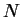 and
and
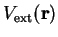 . The ground-state
. The ground-state
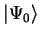 for this Hamiltonian gives
rise to a ground-state electronic density
for this Hamiltonian gives
rise to a ground-state electronic density 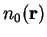
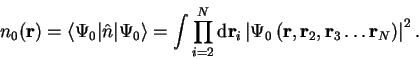 |
(3.4) |
Thus the ground-state
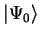 and density
and density
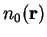 are both functionals of the number of electrons
are both functionals of the number of electrons 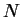 and
the external potential
and
the external potential
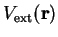 .
Density-functional theory, introduced in 1964 by Hohenberg and Kohn
[16], makes two remarkable statements.
Thus the problem of solving the Schrödinger equation for non-degenerate
ground-states can be recast into a variational problem of minimising the
functional
.
Density-functional theory, introduced in 1964 by Hohenberg and Kohn
[16], makes two remarkable statements.
Thus the problem of solving the Schrödinger equation for non-degenerate
ground-states can be recast into a variational problem of minimising the
functional ![$E_V[n]$](img201.gif) with respect to
with respect to 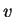 -representable densities.
It should be noted that simple counter-examples of
-representable densities.
It should be noted that simple counter-examples of 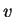 -representable
densities have been found [17,18,19],
but this restriction and the non-degeneracy requirement are overcome by
the constrained search formulation.
-representable
densities have been found [17,18,19],
but this restriction and the non-degeneracy requirement are overcome by
the constrained search formulation.
Following Levy [20,21] we define a functional of the
density 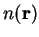 for the operator
for the operator 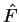 (defined above) as:
(defined above) as:
![\begin{displaymath}
F[n] = \mathop{\rm min}\limits _{\vert \Psi \rangle \rightarrow n}
\langle \Psi \vert {\hat F} \vert \Psi \rangle
\end{displaymath}](img202.gif) |
(3.9) |
i.e. the functional takes the minimum value of the expectation value with
respect to all states
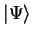 which give the density
which give the density 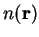 .
For a system with external potential
.
For a system with external potential 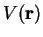 and ground-state
and ground-state
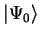 with energy
with energy 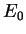 , consider a state
, consider a state
![$\vert \Psi_{[n]} \rangle$](img203.gif) ,
an
,
an 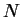 -electron state which yields density
-electron state which yields density 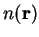 and minimises
and minimises ![$F[n]$](img204.gif) .
Define
.
Define ![$E_V[n]$](img201.gif) as:
as:
![\begin{displaymath}
E_V[n] = F[n] + \int {\mathrm d}{\bf r}~n({\bf r}) V({\bf r}...
...Psi_{[n]} \vert ({\hat F} + {\hat V}) \vert \Psi_{[n]} \rangle
\end{displaymath}](img205.gif) |
(3.10) |
but since
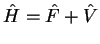 , by the variational
principle we obtain
, by the variational
principle we obtain
![\begin{displaymath}
E_V[n] \geq E_0
\end{displaymath}](img207.gif) |
(3.11) |
with equality only if
![$\vert \Psi_{[n]} \rangle = \vert \Psi_0 \rangle$](img208.gif) . This holds for
all densities which can be obtained from an
. This holds for
all densities which can be obtained from an 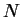 -electron wave-function
(
-electron wave-function
(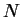 -representable). But from the
definition of
-representable). But from the
definition of ![$F[n]$](img204.gif) (3.9) we must also have
(3.9) we must also have
![\begin{displaymath}
F[n_0] \leq \langle \Psi_0 \vert {\hat F} \vert \Psi_0 \rangle
\end{displaymath}](img209.gif) |
(3.12) |
since
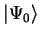 must be one of states which yields
must be one of states which yields 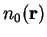 .
Adding
.
Adding
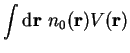 gives
gives
![\begin{displaymath}
E_V[n_0] \leq E_0
\end{displaymath}](img211.gif) |
(3.13) |
which when combined with (3.11) gives the desired result that
![$E_V[n] \geq E_V[n_0] = E_0$](img212.gif) .
.
Thus the ground-state density 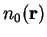 minimises the functional
minimises the functional ![$E_V[n]$](img201.gif) and the minimum value is the ground-state electronic energy. Note that the
requirement for non-degeneracy of the ground-state has disappeared, and
further that instead of considering only
and the minimum value is the ground-state electronic energy. Note that the
requirement for non-degeneracy of the ground-state has disappeared, and
further that instead of considering only 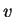 -representable densities, we
can now consider
-representable densities, we
can now consider 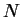 -representable densities. The requirements of
-representable densities. The requirements of
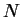 -representability are much weaker and satisfied by any
well-behaved density, indeed the only condition [22] is
proper differentiability i.e. that the quantity
-representability are much weaker and satisfied by any
well-behaved density, indeed the only condition [22] is
proper differentiability i.e. that the quantity
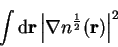
is real and finite.
The remarkable results of density-functional theory are the existence of the
universal functional ![$F[n]$](img204.gif) , which is independent of the external potential,
and that instead of dealing with a function of
, which is independent of the external potential,
and that instead of dealing with a function of 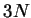 variables (the
many-electron wave-function) we can instead deal with a function of only three
variables (the density). The complexity of the problem has thus been much
reduced, and we note here that this complexity now scales linearly with
system-size
variables (the
many-electron wave-function) we can instead deal with a function of only three
variables (the density). The complexity of the problem has thus been much
reduced, and we note here that this complexity now scales linearly with
system-size 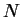 , so that quantum-mechanical calculations based on
density-functional theory can in principle be performed with an effort which
scales linearly with system-size.
, so that quantum-mechanical calculations based on
density-functional theory can in principle be performed with an effort which
scales linearly with system-size.
The exact form of the universal functional ![$F[n]$](img204.gif) is unknown. The Thomas-Fermi
functional [23,24,25]
is unknown. The Thomas-Fermi
functional [23,24,25]
![\begin{displaymath}
F_{\mathrm{TF}}[n] = \frac{3}{10} \left( 3 \pi^2 \right)^{
2...
...bf r}) n({\bf r'})}{\left\vert {\bf r} - {\bf r'} \right\vert}
\end{displaymath}](img215.gif) |
(3.14) |
can, with hindsight, be viewed as a tentative approximation to this
universal functional, but fails to provide even qualitatively correct
predictions for systems other than isolated atoms [26,27] although recent, more accurate developments [28,29,30,31,32]
have led to the implementation of linear-scaling orbital-free methods for
nearly-free electron metals.
The failure to find accurate expressions for the density-functional is a
result of the complexity of the many-body problem which is at the heart of the
definition of the universal functional. For the electron gas, a system of
many interacting particles,
the effects of exchange and correlation are crucial to an accurate
description of its behaviour. In a non-interacting system, the
antisymmetry of the wave-function requires that particles with the same spin
occupy
distinct orthogonal orbitals, and this results in the particles becoming
spatially separated. In an interacting system such as the electron gas
in which all the particles repel each other, exchange will thus lead to a
lowering of the energy. Moreover, the interactions cause the motion of the
particles to become correlated to further reduce the energy of interaction.
Thus it is impossible to treat the electrons as independent particles.
These effects are completely neglected by the Thomas-Fermi model, and must
in part account for its failure, the other source of error being the local approximation for the kinetic energy.
In order to take advantage of the power of DFT without sacrificing accuracy
(i.e. including exchange and correlation effects) we follow the method
of Kohn and Sham [33] to map the problem of the system of
interacting electrons onto a fictitious system of non-interacting ``electrons''.
We write the variational problem for the Hohenberg-Kohn density-functional,
introducing a Lagrange multiplier 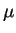 to constrain the number of
electrons to be
to constrain the number of
electrons to be 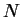 :
:
![\begin{displaymath}
\delta \left[ F[n] + \int {\mathrm d}{\bf r}~V_{\mathrm{ext}...
...( \int {\mathrm d}{\bf r}~n({\bf r}) - N \right)
\right] = 0 .
\end{displaymath}](img217.gif) |
(3.15) |
Kohn and Sham separated ![$F[n]$](img204.gif) into three parts
into three parts
![\begin{displaymath}
F[n] = T_{\mathrm s}[n] + \frac{1}{2} \int {\mathrm d}{\bf r...
...left\vert {\bf r} - {\bf r'}
\right\vert} + E_{\mathrm{xc}}[n]
\end{displaymath}](img218.gif) |
(3.16) |
in which
![$T_{\mathrm s}[n]$](img219.gif) is defined as the kinetic energy of a
non-interacting gas with density
is defined as the kinetic energy of a
non-interacting gas with density 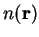 (not the same as that of the
interacting system, although we might hope that the two quantities were of
the same order of magnitude), the second term is the classical electrostatic
(Hartree) energy and the final term is an implicit definition of the
exchange-correlation energy which contains the non-classical electrostatic
interaction energy and the difference between the kinetic energies of
the interacting and non-interacting systems. The aim of this separation is
that the first two terms can be dealt with simply, and the last term, which
contains the effects of the complex behaviour, is a small fraction of the
total energy and can be approximated surprisingly well.
(not the same as that of the
interacting system, although we might hope that the two quantities were of
the same order of magnitude), the second term is the classical electrostatic
(Hartree) energy and the final term is an implicit definition of the
exchange-correlation energy which contains the non-classical electrostatic
interaction energy and the difference between the kinetic energies of
the interacting and non-interacting systems. The aim of this separation is
that the first two terms can be dealt with simply, and the last term, which
contains the effects of the complex behaviour, is a small fraction of the
total energy and can be approximated surprisingly well.
Using this separation, equation 3.15 can be rewritten:
![\begin{displaymath}
\frac{\delta T_{\mathrm s}[n]}{\delta n({\bf r})} + V_{\mathrm{KS}}({\bf r}) =
\mu
\end{displaymath}](img220.gif) |
(3.17) |
in which the Kohn-Sham potential
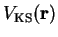 is given by
is given by
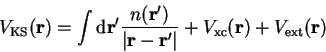 |
(3.18) |
and the exchange-correlation potential
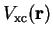 is
is
![\begin{displaymath}
V_{\mathrm{xc}}({\bf r}) = \frac{ \delta E_{\mathrm{xc}}[n] }
{ \delta n({\bf r}) } .
\end{displaymath}](img224.gif) |
(3.19) |
The crucial point to note here is that equation 3.17 is
precisely the same equation
which would be obtained for a non-interacting system of particles moving in
an external potential
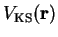 . To find the ground-state
density
. To find the ground-state
density
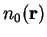 for this non-interacting system we simply solve the one-electron
Schrödinger equations;
for this non-interacting system we simply solve the one-electron
Schrödinger equations;
![\begin{displaymath}
\left[ -\textstyle{1 \over 2} \nabla^2 + V_{\mathrm{KS}}({\bf r}) \right]
\psi_i({\bf r}) = \varepsilon_i \psi_i({\bf r})
\end{displaymath}](img225.gif) |
(3.20) |
for
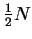 single-particle states3.1
single-particle states3.1
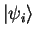 with
energies
with
energies 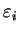 , constructing the density from
, constructing the density from
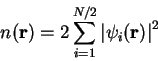 |
(3.21) |
(the factor 2 is for spin degeneracy - we assume the orbitals are
singly-occupied) and the non-interacting kinetic energy
![$T_{\mathrm s}[n]$](img219.gif) from
from
![\begin{displaymath}
T_{\mathrm s}[n] = - \sum_{i=1}^{N/2}
\int {\mathrm d}{\bf r}~\psi_i^{\ast}({\bf r}) \nabla^2 \psi_i({\bf r}) .
\end{displaymath}](img230.gif) |
(3.22) |
Since the Kohn-Sham potential
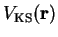 depends upon the
density
depends upon the
density
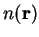 it is necessary to solve these equations self-consistently
i.e. having made a guess for the form of the density, the Schrödinger
equation is solved to obtain a set of orbitals
it is necessary to solve these equations self-consistently
i.e. having made a guess for the form of the density, the Schrödinger
equation is solved to obtain a set of orbitals
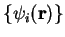 from
which a new density is constructed, and the process repeated until the input
and output densities are the same. In practice there is no problem
converging to the ground-state minimum because of the convex nature of the
density-functional [34].
from
which a new density is constructed, and the process repeated until the input
and output densities are the same. In practice there is no problem
converging to the ground-state minimum because of the convex nature of the
density-functional [34].
The energy of the non-interacting system, the sum of one-electron
eigenvalues, is
which, compared to the interacting system, double-counts the Hartree energy and
over-counts the exchange-correlation energy so that the interacting
energy is
![\begin{displaymath}
E = 2 \sum_{i=1}^{N/2} \varepsilon_i - \frac{1}{2} \int {\ma...
... r}~n({\bf r}) V_{\mathrm{xc}}({\bf r}) +
E_{\mathrm{xc}}[n] .
\end{displaymath}](img235.gif) |
(3.24) |
Direct solution of the Schrödinger equation for the
extended non-interacting
orbitals
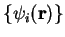 requires a computational effort which scales
as the cube of the system-size
requires a computational effort which scales
as the cube of the system-size 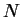 , due to the cost of diagonalising the
Hamiltonian or orthogonalising the orbitals, whereas the original complexity of
finding a minimum of the Hohenberg-Kohn functional only required an effort
which scaled linearly with
, due to the cost of diagonalising the
Hamiltonian or orthogonalising the orbitals, whereas the original complexity of
finding a minimum of the Hohenberg-Kohn functional only required an effort
which scaled linearly with 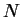 . Thus a linear-scaling method must modify
this Kohn-Sham scheme.
. Thus a linear-scaling method must modify
this Kohn-Sham scheme.
The results so far are exact, provided that the functional form of
![$E_{\mathrm{xc}}[n]$](img236.gif) is
known. The problem of determining the functional form of the universal
Hohenberg-Kohn density functional has now been transferred to this one term,
and therefore this term is not known exactly.
Remarkably, it is possible to make simple approximations for the
exchange-correlation energy which work extremely well, and the simplest of
these, which is the approximation adopted in this work, is the local
density approximation (LDA).
is
known. The problem of determining the functional form of the universal
Hohenberg-Kohn density functional has now been transferred to this one term,
and therefore this term is not known exactly.
Remarkably, it is possible to make simple approximations for the
exchange-correlation energy which work extremely well, and the simplest of
these, which is the approximation adopted in this work, is the local
density approximation (LDA).
In the LDA, the contribution to the exchange-correlation energy from each
infinitesimal volume in space,
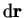 , is taken to be the value
it would have if the whole of space were filled with a homogeneous electron
gas with the same density as is found in
, is taken to be the value
it would have if the whole of space were filled with a homogeneous electron
gas with the same density as is found in
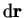 i.e.
i.e.
![\begin{displaymath}
E_{\mathrm{xc}}[n] = \int {\mathrm d}{\bf r}~\epsilon_{\mathrm{xc}}\left(
n({\bf r})\right)
n({\bf r})
\end{displaymath}](img238.gif) |
(3.25) |
where
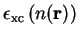 is the
exchange-correlation energy per electron in a homogeneous electron gas of
density
is the
exchange-correlation energy per electron in a homogeneous electron gas of
density 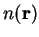 . The exchange-correlation potential
. The exchange-correlation potential
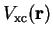 then takes the form
then takes the form
![\begin{displaymath}
V_{\mathrm{xc}}({\bf r}) = \frac{\delta E_{\mathrm{xc}}[n]}{...
...c}}\left(n\right)}{{\mathrm d}n} \right\vert _{n=n({\bf r})} .
\end{displaymath}](img240.gif) |
(3.26) |
The exchange-correlation energy for the homogeneous electron gas has been
calculated by Ceperley and Alder [35] using Monte Carlo
methods
and in this work we use a parameterisation by Perdew and Zunger
[36]. The LDA is exact in the limit of slowly-varying
densities, however, the density in systems of interest is generally rapidly
varying, and the LDA would appear to be a crude approximation in these
cases. Its use is justified a posteriori by its surprising success
at predicting physical properties in real systems.
This success may be due in part to the fact that the sum rule for the
exchange-correlation hole, which must be obeyed by the real functional, is
reproduced by the LDA [37].
We can connect the interacting and non-interacting
systems using a variable coupling constant 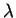 which varies between 0
and 1.
We replace the Coulomb interaction by
which varies between 0
and 1.
We replace the Coulomb interaction by
and vary 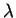 in the presence of an external potential
in the presence of an external potential
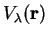 so that the ground-state density for all values of
so that the ground-state density for all values of 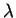 is the same
[38].
The Hamiltonian is therefore
is the same
[38].
The Hamiltonian is therefore
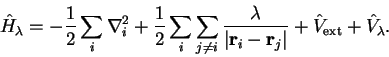 |
(3.27) |
The exchange-correlation hole
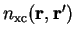 is
then
defined in terms of a coupling-constant integration of the pair
correlation function
is
then
defined in terms of a coupling-constant integration of the pair
correlation function
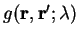 of the system with
density
of the system with
density 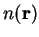 and scaled Coulomb interaction
[39,40];
and scaled Coulomb interaction
[39,40];
![\begin{displaymath}
n_{\mathrm{xc}}({\bf r},{\bf r'}) = n({\bf r'}) \int_0^1
{\mathrm d}\lambda \left[ g({\bf r},{\bf r'};\lambda) - 1 \right] .
\end{displaymath}](img247.gif) |
(3.28) |
The exchange-correlation energy can then be expressed in the form of a
classical electrostatic interaction between the density 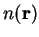 and
the hole density
and
the hole density
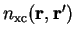 ;
;
![\begin{displaymath}
E_{\mathrm{xc}}[n] = \frac{1}{2} \int {\mathrm d}{\bf r}~{\m...
...bf r},{\bf r'})}
{\left\vert {\bf r} - {\bf r'} \right\vert} .
\end{displaymath}](img248.gif) |
(3.29) |
The sum rule follows from the definition of the pair correlation function
[41]
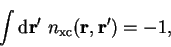 |
(3.30) |
which is interpreted by saying that the exchange-correlation hole
excludes one electron as expected. It can also be shown that the exchange-correlation energy
depends only weakly on the detailed shape of the exchange-correlation hole
[42], and these two facts account, at least in part,
for the success of the LDA.
This view is supported by the fact that improvements to the LDA involving
gradient expansions show no consistent improvement unless they enforce the sum
rule obeyed by the LDA [43,44].




Next: 3.2 Periodic systems
Up: 3. Quantum Mechanics of
Previous: 3. Quantum Mechanics of
Contents
Peter Haynes
![]() . We
deal with a system of
. We
deal with a system of ![]() electrons moving in a static potential, and adopt
a conventional normalisation in which
electrons moving in a static potential, and adopt
a conventional normalisation in which
![]() .
.
![]() :
:
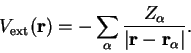
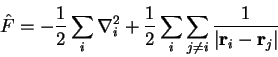
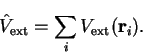
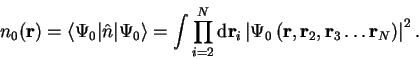
![]() with ground-state
with ground-state
![]() gives rise to the same density
gives rise to the same density ![]() . The ground-state energies are
. The ground-state energies are
![]() and
and
![]() where
where
![]() and
and
![]() . Taking
. Taking
![]() as a trial wave-function for the Hamiltonian
as a trial wave-function for the Hamiltonian ![]() , we obtain
the strict inequality
, we obtain
the strict inequality
![$\displaystyle E_0' +
\int {\mathrm d}{\bf r} ~n_0({\bf r}) \left[ V_{\mathrm{ext}}({\bf r}) -
V_{\mathrm{ext}}'({\bf r}) \right] ,$](img187.gif)
![$\displaystyle E_0 -
\int {\mathrm d}{\bf r} ~n_0({\bf r}) \left[ V_{\mathrm{ext}}({\bf r}) -
V_{\mathrm{ext}}'({\bf r}) \right]$](img191.gif)
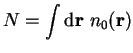 determine
all the ground-state properties of the system since the Hamiltonian
and ground-state wave-function are determined by them.
determine
all the ground-state properties of the system since the Hamiltonian
and ground-state wave-function are determined by them.
![]() which are ground-state densities for some
external potential (
which are ground-state densities for some
external potential (![]() -representable) the functional
-representable) the functional
![]() is unique and well-defined, since
is unique and well-defined, since
![]() determines the external potential and
determines the external potential and ![]() (and therefore
(and therefore ![]() ) and thence
) and thence
![]() . Now a functional for an arbitrary external potential
. Now a functional for an arbitrary external potential ![]() unrelated to the
unrelated to the
![]() determined by
determined by ![]() can be defined:
can be defined:
![]() determines its own external potential
determines its own external potential
![]() and ground-state
and ground-state
![]() . If this state is used as a trial state
for the Hamiltonian with external potential
. If this state is used as a trial state
for the Hamiltonian with external potential ![]() , we have
, we have
![]() for the operator
for the operator ![]() (defined above) as:
(defined above) as:
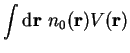 gives
gives
![]() minimises the functional
minimises the functional ![]() and the minimum value is the ground-state electronic energy. Note that the
requirement for non-degeneracy of the ground-state has disappeared, and
further that instead of considering only
and the minimum value is the ground-state electronic energy. Note that the
requirement for non-degeneracy of the ground-state has disappeared, and
further that instead of considering only ![]() -representable densities, we
can now consider
-representable densities, we
can now consider ![]() -representable densities. The requirements of
-representable densities. The requirements of
![]() -representability are much weaker and satisfied by any
well-behaved density, indeed the only condition [22] is
proper differentiability i.e. that the quantity
-representability are much weaker and satisfied by any
well-behaved density, indeed the only condition [22] is
proper differentiability i.e. that the quantity
![]() , which is independent of the external potential,
and that instead of dealing with a function of
, which is independent of the external potential,
and that instead of dealing with a function of ![]() variables (the
many-electron wave-function) we can instead deal with a function of only three
variables (the density). The complexity of the problem has thus been much
reduced, and we note here that this complexity now scales linearly with
system-size
variables (the
many-electron wave-function) we can instead deal with a function of only three
variables (the density). The complexity of the problem has thus been much
reduced, and we note here that this complexity now scales linearly with
system-size ![]() , so that quantum-mechanical calculations based on
density-functional theory can in principle be performed with an effort which
scales linearly with system-size.
, so that quantum-mechanical calculations based on
density-functional theory can in principle be performed with an effort which
scales linearly with system-size.
![]() is unknown. The Thomas-Fermi
functional [23,24,25]
is unknown. The Thomas-Fermi
functional [23,24,25]
![\begin{displaymath}
F_{\mathrm{TF}}[n] = \frac{3}{10} \left( 3 \pi^2 \right)^{
2...
...bf r}) n({\bf r'})}{\left\vert {\bf r} - {\bf r'} \right\vert}
\end{displaymath}](img215.gif)
![]() to constrain the number of
electrons to be
to constrain the number of
electrons to be ![]() :
:
![\begin{displaymath}
F[n] = T_{\mathrm s}[n] + \frac{1}{2} \int {\mathrm d}{\bf r...
...left\vert {\bf r} - {\bf r'}
\right\vert} + E_{\mathrm{xc}}[n]
\end{displaymath}](img218.gif)
![\begin{displaymath}
V_{\mathrm{xc}}({\bf r}) = \frac{ \delta E_{\mathrm{xc}}[n] }
{ \delta n({\bf r}) } .
\end{displaymath}](img224.gif)
![]() . To find the ground-state
density
. To find the ground-state
density
![]() for this non-interacting system we simply solve the one-electron
Schrödinger equations;
for this non-interacting system we simply solve the one-electron
Schrödinger equations;
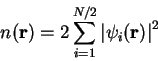
![\begin{displaymath}
T_{\mathrm s}[n] = - \sum_{i=1}^{N/2}
\int {\mathrm d}{\bf r}~\psi_i^{\ast}({\bf r}) \nabla^2 \psi_i({\bf r}) .
\end{displaymath}](img230.gif)
![]() depends upon the
density
depends upon the
density
![]() it is necessary to solve these equations self-consistently
i.e. having made a guess for the form of the density, the Schrödinger
equation is solved to obtain a set of orbitals
it is necessary to solve these equations self-consistently
i.e. having made a guess for the form of the density, the Schrödinger
equation is solved to obtain a set of orbitals
![]() from
which a new density is constructed, and the process repeated until the input
and output densities are the same. In practice there is no problem
converging to the ground-state minimum because of the convex nature of the
density-functional [34].
from
which a new density is constructed, and the process repeated until the input
and output densities are the same. In practice there is no problem
converging to the ground-state minimum because of the convex nature of the
density-functional [34].
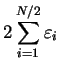
![$\displaystyle T_{\mathrm s}[n] + \int {\mathrm d}{\bf r}~
n({\bf r}) V_{\mathrm{KS}}({\bf r})$](img233.gif)
![$\displaystyle T_{\mathrm s}[n] + \int {\mathrm d}{\bf r}~{\mathrm d}{\bf r'}~
\...
...rm{xc}}({\bf r})
+ \int {\mathrm d}{\bf r}~n({\bf r}) V_{\mathrm{ext}}({\bf r})$](img234.gif)
![\begin{displaymath}
E = 2 \sum_{i=1}^{N/2} \varepsilon_i - \frac{1}{2} \int {\ma...
... r}~n({\bf r}) V_{\mathrm{xc}}({\bf r}) +
E_{\mathrm{xc}}[n] .
\end{displaymath}](img235.gif)
![]() requires a computational effort which scales
as the cube of the system-size
requires a computational effort which scales
as the cube of the system-size ![]() , due to the cost of diagonalising the
Hamiltonian or orthogonalising the orbitals, whereas the original complexity of
finding a minimum of the Hohenberg-Kohn functional only required an effort
which scaled linearly with
, due to the cost of diagonalising the
Hamiltonian or orthogonalising the orbitals, whereas the original complexity of
finding a minimum of the Hohenberg-Kohn functional only required an effort
which scaled linearly with ![]() . Thus a linear-scaling method must modify
this Kohn-Sham scheme.
. Thus a linear-scaling method must modify
this Kohn-Sham scheme.
![]() is
known. The problem of determining the functional form of the universal
Hohenberg-Kohn density functional has now been transferred to this one term,
and therefore this term is not known exactly.
Remarkably, it is possible to make simple approximations for the
exchange-correlation energy which work extremely well, and the simplest of
these, which is the approximation adopted in this work, is the local
density approximation (LDA).
is
known. The problem of determining the functional form of the universal
Hohenberg-Kohn density functional has now been transferred to this one term,
and therefore this term is not known exactly.
Remarkably, it is possible to make simple approximations for the
exchange-correlation energy which work extremely well, and the simplest of
these, which is the approximation adopted in this work, is the local
density approximation (LDA).
![]() , is taken to be the value
it would have if the whole of space were filled with a homogeneous electron
gas with the same density as is found in
, is taken to be the value
it would have if the whole of space were filled with a homogeneous electron
gas with the same density as is found in
![]() i.e.
i.e. ![\begin{displaymath}
V_{\mathrm{xc}}({\bf r}) = \frac{\delta E_{\mathrm{xc}}[n]}{...
...c}}\left(n\right)}{{\mathrm d}n} \right\vert _{n=n({\bf r})} .
\end{displaymath}](img240.gif)
![]() which varies between 0
and 1.
We replace the Coulomb interaction by
which varies between 0
and 1.
We replace the Coulomb interaction by
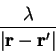
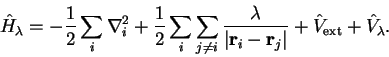
![\begin{displaymath}
E_{\mathrm{xc}}[n] = \frac{1}{2} \int {\mathrm d}{\bf r}~{\m...
...bf r},{\bf r'})}
{\left\vert {\bf r} - {\bf r'} \right\vert} .
\end{displaymath}](img248.gif)