In this paper, whenever we refer to `delta functions' we will assume a periodic and bandwidth limited version of the Dirac delta functions. These delta functions are three-dimensional versions of the `impulse functions' that are common in signal processing applications of FFTs [53]. In electronic structure, similar functions have been used as `mesh delta functions' in the `exact finite difference method' of Hoshi et al. [54] and in recent studies of their possible application when we consider the limit of an infinite simulation cell [55].
In our derivations we will assume that we have a simulation cell of any
symmetry, which in general is a parallelepiped defined by its primitive
lattice vectors ![]() ,
, ![]() and
and ![]() .
In this simulation cell we define a regular grid
with an odd number of points
.
In this simulation cell we define a regular grid
with an odd number of points ![]() ,
, ![]() , and
, and ![]() in every direction (the adaptation of our results to the case
of even numbers of points is straightforward). Therefore
point
in every direction (the adaptation of our results to the case
of even numbers of points is straightforward). Therefore
point
![]() of this regular grid is defined as
of this regular grid is defined as
| (31) |
Bandwidth limited delta functions centred at points of the regular
grid are defined as
| (33) |
| (34) |
![\scalebox{0.6}{\includegraphics*[3cm,0cm][28cm,20cm]{delta_15_15_BW.eps}}](img163.png)
|
The delta functions act as Dirac delta functions with the
added effect of filtering out any plane-wave components
that are not part of them. For example, if ![]() is a
function periodic with the periodicity of the simulation cell
but not bandwidth limited, it can be expressed in terms of
its discrete Fourier transform (plane-wave) expansion
is a
function periodic with the periodicity of the simulation cell
but not bandwidth limited, it can be expressed in terms of
its discrete Fourier transform (plane-wave) expansion
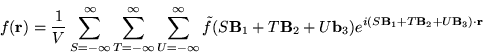 |
(35) |
It is straightforward to show that the projection of
![]() onto
onto
![]() is
is
As the NGWFs are linear combinations of the delta functions
according to (7), the result of equation (36)
is very important since it leads to the following relation
As a corollary we observe that the delta functions are an
orthogonal set since
We also need to define the fine grid delta functions
![]() (here the
(here the ![]() are just grid point indices for the fine grid, they are
not related to any Cartesian coordinates). These functions
are the analogues of the delta functions we have just described that
would be obtained if we doubled the minimum and maximum values
that their wavevectors can take. Consequently, they
have the same periodicity but they correspond to a grid with twice the
number of points in every direction,
i.e.
are just grid point indices for the fine grid, they are
not related to any Cartesian coordinates). These functions
are the analogues of the delta functions we have just described that
would be obtained if we doubled the minimum and maximum values
that their wavevectors can take. Consequently, they
have the same periodicity but they correspond to a grid with twice the
number of points in every direction,
i.e. ![]() ,
, ![]() and
and ![]() points. They are defined by
points. They are defined by
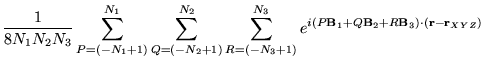 |
(38) |
| (39) |