

Next: Total energy optimisation
Up: Nonorthogonal generalized Wannier function
Previous: Introduction
Charge density and total electronic energy with
Non-orthogonal Generalised Wannier functions
Linear-scaling DFT calculations are aimed at large systems, and in
particular, large unit cells. Thus in this work we will be concerned
with calculations only at the  -point, i.e.
-point, i.e.
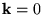 . This means that the Bloch bands and therefore the
NGWFs can be chosen to be real. We can also drop the dependence of
the NGWFs on
. This means that the Bloch bands and therefore the
NGWFs can be chosen to be real. We can also drop the dependence of
the NGWFs on 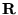 , so that
, so that
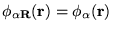 .
.
Our basis set is the set of periodic bandwidth limited delta functions
that are centred on the points
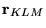 of a regular
real-space grid:
of a regular
real-space grid:
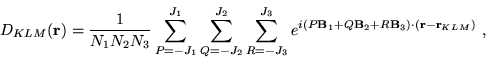 |
(5) |
where 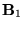 is one of the reciprocal
lattice vectors of the simulation cell.
is one of the reciprocal
lattice vectors of the simulation cell.
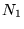 is the number of grid points in the direction
of direct lattice vector
is the number of grid points in the direction
of direct lattice vector 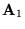 , and
, and 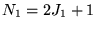 .
The delta function basis is equivalent to the
plane-waves that can be represented
by the real-space grid since it is related to
them via a unitary transformation. An important property
of the basis set is that the projection of a function
.
The delta function basis is equivalent to the
plane-waves that can be represented
by the real-space grid since it is related to
them via a unitary transformation. An important property
of the basis set is that the projection of a function
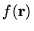 on
on
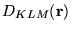 is
is
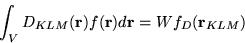 |
(6) |
where 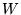 is the volume per grid point and
is the volume per grid point and
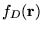 is the result of bandwidth limiting the function
is the result of bandwidth limiting the function 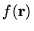 to the same plane-wave components as in (5).
to the same plane-wave components as in (5).
We represent the NGWFs in the delta function basis by
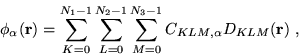 |
(7) |
and in the plane-wave basis by
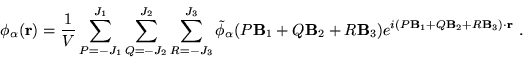 |
(8) |
where it is straightforward to show that the amplitudes
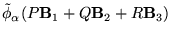 are the result of a discrete Fourier transform on the
delta function expansion coefficients
are the result of a discrete Fourier transform on the
delta function expansion coefficients
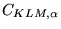 .
.
In (7) the sum over the 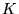 ,
, 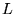 and
and 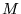 indices
formally goes over the grid points of a regular grid
that extends over the whole simulation cell.
From now on however, we will restrict all NGWFs to have contributions
only from delta functions centred inside a predefined
spherical region. This spherical region is in general different
for each NGWF.
Thus we impose on (7) the condition:
indices
formally goes over the grid points of a regular grid
that extends over the whole simulation cell.
From now on however, we will restrict all NGWFs to have contributions
only from delta functions centred inside a predefined
spherical region. This spherical region is in general different
for each NGWF.
Thus we impose on (7) the condition:
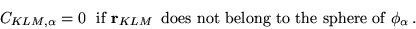 |
(9) |
This of course does not affect the form or the applicability
of equation (8).
The charge density of equation (2) with our
NGWFs becomes (from now on we will use the summation convention
for repeated Greek indices)
which involves the fine grid delta functions
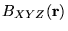 that are defined in a similar way to the
that are defined in a similar way to the
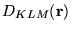 of
equation (5) but include up to twice the maximum
wavevector of
of
equation (5) but include up to twice the maximum
wavevector of
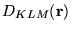 in every reciprocal lattice
vector direction (see also Appendix A). This is
necessary because a
product of two
in every reciprocal lattice
vector direction (see also Appendix A). This is
necessary because a
product of two
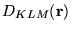 delta functions is a linear
combination of fine grid delta functions
delta functions is a linear
combination of fine grid delta functions
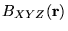 ,
a result reminiscent of the Gaussian function product
rule [30].
,
a result reminiscent of the Gaussian function product
rule [30].
The expressions for the various contributions to the total electronic energy
with the NGWFs are simple to derive from
(10). The total energy is the sum of the kinetic energy 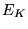 ,
the Hartree energy
,
the Hartree energy 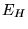 , the local pseudopotential energy
, the local pseudopotential energy 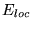 ,
the non-local pseudopotential energy
,
the non-local pseudopotential energy 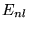 and the
exchange and correlation energy
and the
exchange and correlation energy 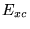
![\begin{displaymath}
E[n]= E_{K}[n] + E_{H}[n]+ E_{loc}[n] + E_{nl}[n]
+ E_{xc}[n] \,\, .
\end{displaymath}](img65.png) |
(11) |
The kinetic energy is written as a trace of the product
of the density kernel and of the matrix
elements of the kinetic energy operator
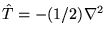
![\begin{displaymath}
E_{K}[n] = 2 K^{\alpha \beta} \langle \phi_{\beta} \vert
\hat{T} \vert \phi_{\alpha} \rangle .
\end{displaymath}](img67.png) |
(12) |
To compute these matrix elements we can apply
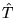 to the plane-wave representation
(8) of
to the plane-wave representation
(8) of
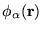 and then evaluate the
integral in real-space where it is equal to a discrete sum over grid points
where
and then evaluate the
integral in real-space where it is equal to a discrete sum over grid points
where
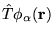 obviously plays the role
of
obviously plays the role
of
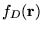 of equation (6).
of equation (6).
Calculation of the Hartree energy requires first the Hartree
potential. From equation (10) we see that the charge
density is a fine grid delta function expansion, thus the same should
be true for the Hartree potential, which is a convolution of the
charge density with the Coulomb potential. Therefore,
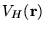 can be written as a linear combination of fine grid delta functions
and extends over the whole simulation cell:
can be written as a linear combination of fine grid delta functions
and extends over the whole simulation cell:
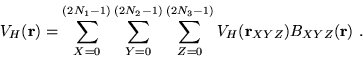 |
(13) |
The Hartree energy is
![\begin{displaymath}
E_{H}[n]= \frac{1}{2}\int V_{H}(\mathbf{r}) n(\mathbf{r}) d\...
...langle \phi_{\beta} \vert V_{H} \vert
\phi_{\alpha} \rangle .
\end{displaymath}](img73.png) |
(14) |
This quantity can be calculated as a discrete summation on the fine
grid of the product of
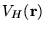 with
with
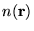 or equivalently as a trace
of the product of the density kernel and the potential matrix
elements. The local potential matrix elements are integrals that
are identically equal to discrete sums on the regular grid
provided of course that
or equivalently as a trace
of the product of the density kernel and the potential matrix
elements. The local potential matrix elements are integrals that
are identically equal to discrete sums on the regular grid
provided of course that
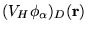 is first put on the regular grid.
is first put on the regular grid.
The local pseudopotential energy is calculated in an entirely analogous manner
to the Hartree energy and can be represented by equation
(14) if we put 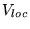 in place of
in place of 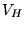 and multiply
it by a factor of 2 to take into account the lack of self-interaction
in this case.
and multiply
it by a factor of 2 to take into account the lack of self-interaction
in this case.
The non-local pseudopotential energy ![$ E_{nl}[n] $](img78.png) is the expectation
value of the non-local potential operator
is the expectation
value of the non-local potential operator
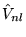 in the Kleinman-Bylander form [31]:
in the Kleinman-Bylander form [31]:
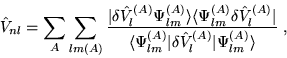 |
(15) |
where the 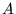 -summation runs over the atoms in the system
and the
-summation runs over the atoms in the system
and the 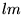 -summation runs over the pseudo-atomic orbitals of a
particular atom. The
-summation runs over the pseudo-atomic orbitals of a
particular atom. The
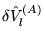 is an angular momentum
dependent component of the non-local potential of a pseudo-Hamiltonian for
a particular atom and the
is an angular momentum
dependent component of the non-local potential of a pseudo-Hamiltonian for
a particular atom and the
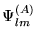 are the atomic pseudo-orbitals
associated with it.
In the NGWF representation the non-local potential energy is again expressed
as a matrix trace:
are the atomic pseudo-orbitals
associated with it.
In the NGWF representation the non-local potential energy is again expressed
as a matrix trace:
![\begin{displaymath}
E_{nl}[n]=2 K^{\alpha \beta} \langle \phi_{\beta} \vert
\hat{V}_{nl} \vert \phi_{\alpha} \rangle \, .
\end{displaymath}](img85.png) |
(16) |
The
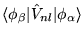 matrix elements require the calculation of overlap integrals
matrix elements require the calculation of overlap integrals
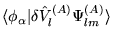 between the NGWFs and the non-local projectors
between the NGWFs and the non-local projectors
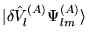 .
These are simple to compute as discrete summations on the regular
grid, starting from the plane-wave representation of the
non-local projectors which is analogous to the plane-wave
representation of the NGWFs in equation (8).
These integrals need only be calculated when the sphere of
function
.
These are simple to compute as discrete summations on the regular
grid, starting from the plane-wave representation of the
non-local projectors which is analogous to the plane-wave
representation of the NGWFs in equation (8).
These integrals need only be calculated when the sphere of
function
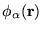 overlaps the core of
atom
overlaps the core of
atom 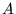 .
.
The exchange-correlation energy is obtained by
approximating the exchange-correlation functional expression
as a direct summation on the fine grid, which first involves
the evaluation of a function
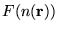 whose particular
form depends on our choice of
exchange-correlation functional[2]:
whose particular
form depends on our choice of
exchange-correlation functional[2]:
![\begin{displaymath}
E_{xc}[n]=\int_{V} F(n(\mathbf{r})) d \mathbf{r}
\simeq \frac{V}{8N_1 N_2 N_3}
\sum_{XYZ} F(n(\mathbf{r}_{XYZ}) ) \,\, .
\end{displaymath}](img90.png) |
(17) |
This is the only approximation in integral evaluation in our
method as all direct summations described up
to now were exactly equal to the analytic integrals.
However, in the case of the exchange-correlation energy,
the exchange-correlation functionals usually contain highly
non-linear expressions that can not be
represented without any aliasing even
when we use the delta functions of the fine grid.
The resulting errors however will be of
the same nature as in conventional plane-wave codes and
therefore negligible [1].


Next: Total energy optimisation
Up: Nonorthogonal generalized Wannier function
Previous: Introduction
Peter D. Haynes
2002-10-31
![]() -point, i.e.
-point, i.e.
![]() . This means that the Bloch bands and therefore the
NGWFs can be chosen to be real. We can also drop the dependence of
the NGWFs on
. This means that the Bloch bands and therefore the
NGWFs can be chosen to be real. We can also drop the dependence of
the NGWFs on ![]() , so that
, so that
![]() .
.
![]() of a regular
real-space grid:
of a regular
real-space grid:
![]() ,
, ![]() and
and ![]() indices
formally goes over the grid points of a regular grid
that extends over the whole simulation cell.
From now on however, we will restrict all NGWFs to have contributions
only from delta functions centred inside a predefined
spherical region. This spherical region is in general different
for each NGWF.
Thus we impose on (7) the condition:
indices
formally goes over the grid points of a regular grid
that extends over the whole simulation cell.
From now on however, we will restrict all NGWFs to have contributions
only from delta functions centred inside a predefined
spherical region. This spherical region is in general different
for each NGWF.
Thus we impose on (7) the condition:
![]() ,
the Hartree energy
,
the Hartree energy ![]() , the local pseudopotential energy
, the local pseudopotential energy ![]() ,
the non-local pseudopotential energy
,
the non-local pseudopotential energy ![]() and the
exchange and correlation energy
and the
exchange and correlation energy ![]()
![]() can be written as a linear combination of fine grid delta functions
and extends over the whole simulation cell:
can be written as a linear combination of fine grid delta functions
and extends over the whole simulation cell:
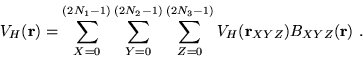
![]() in place of
in place of ![]() and multiply
it by a factor of 2 to take into account the lack of self-interaction
in this case.
and multiply
it by a factor of 2 to take into account the lack of self-interaction
in this case.
![]() is the expectation
value of the non-local potential operator
is the expectation
value of the non-local potential operator
![]() in the Kleinman-Bylander form [31]:
in the Kleinman-Bylander form [31]:
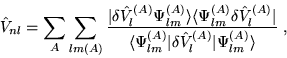
![]() whose particular
form depends on our choice of
exchange-correlation functional[2]:
whose particular
form depends on our choice of
exchange-correlation functional[2]: