

Next: The FFT box technique
Up: Nonorthogonal generalized Wannier function
Previous: Charge density and total
Total energy optimisation
The total energy is a functional of the charge density
![$E[n]$](img91.png) . From equation (10) we see that
the charge density is expanded in fine grid delta functions where
. From equation (10) we see that
the charge density is expanded in fine grid delta functions where
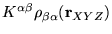 are the expansion coefficients. Therefore the energy will
have a variational dependence on these coefficients
provided they form an
are the expansion coefficients. Therefore the energy will
have a variational dependence on these coefficients
provided they form an 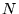 -representable charge density.
Consequently, the energy should also have a variational dependence
on the density kernel
-representable charge density.
Consequently, the energy should also have a variational dependence
on the density kernel
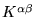 and the
NGWF expansion coefficients
and the
NGWF expansion coefficients
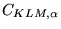 since the
since the
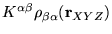 are constructed from them
are constructed from them
![\begin{displaymath}
E[n]=E( \{ K^{\alpha \beta} \}, \{ C_{KLM,\alpha} \} ) \,\, .
\end{displaymath}](img94.png) |
(18) |
It is thus sufficient to minimise the energy with respect
to
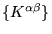 and
and
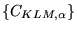 . We must however do this under two
constraints. The first is that the number of
electrons corresponding to the charge density
. We must however do this under two
constraints. The first is that the number of
electrons corresponding to the charge density
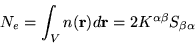 |
(19) |
should remain constant. The second is that
the ground state density matrix should be idempotent, or in other words
the eigenfunctions of the Kohn-Sham Hamiltonian have to
be orthonormal
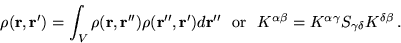 |
(20) |
We choose to carry out the total energy minimisation in
two nested loops, in a fashion similar to the ensemble
DFT method of Marzari et al. [32].
The density kernel will play the role of the generalised
occupation numbers and the NWGFs will play the role
of the orbitals. So we can reach the minimum energy
in two constrained-search stages:
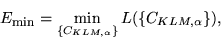 |
(21) |
with
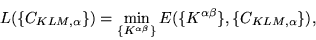 |
(22) |
where the minimisation with respect to the density kernel
in equation (22) ensures that 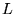 of equation
(21) is a function of the NGWF coefficients only.
In practice in equation (22) we do not just minimise
the energy with respect to
of equation
(21) is a function of the NGWF coefficients only.
In practice in equation (22) we do not just minimise
the energy with respect to
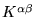 but we also
impose the electron number and idempotency
constraints (19) and (20).
There are a variety of efficient methods for achieving
this available in the literature, derived from the need
to perform linear-scaling calculations with
a localised basis [9,10,33,34,35].
Any of these methods would ensure that
the density kernel in (22)
adapts to the current NGWFs so that it minimises
the energy within the imposed constraints.
but we also
impose the electron number and idempotency
constraints (19) and (20).
There are a variety of efficient methods for achieving
this available in the literature, derived from the need
to perform linear-scaling calculations with
a localised basis [9,10,33,34,35].
Any of these methods would ensure that
the density kernel in (22)
adapts to the current NGWFs so that it minimises
the energy within the imposed constraints.
In the present work we have used the variant
of the Li, Nunes and Vanderbilt (LNV)[9] method
that was developed by Millam and Scuseria[36] in calculations with
Gaussian basis sets. We emphasise again, though, that any
of the other available methods could have been used
as well. For simplicity
of presentation, our analysis from now on will assume that
the energy of equation (22) is minimised without any
constraints. In order to take into account the constraints,
the formulae we derive will have to be modified
according to the density kernel minimisation method one
chooses to use. This is a straightforward but tedious exercise [37].
The minimisation of equation (22) can be performed
iteratively with the conjugate gradients method [38].
As in the simpler steepest descents method, the essential
ingredient is the gradient. It is easy to show [39] that
this quantity is equal to twice the matrix elements of the
Kohn-Sham Hamiltonian
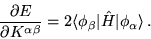 |
(23) |
The non-orthogonality of our NGWFs has to be taken into
account when computing search directions with the above
gradient by transforming it to a
contravariant second order tensor [40,41].
The minimisation stage of equation (21)
is also performed iteratively with the conjugate gradients method.
In this case, one can show by using the properties
of the delta function basis set that the gradient is:
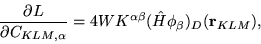 |
(24) |
where 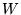 is the weight associated with each grid point.
Here a contravariant-to-covariant
tensor correction is needed when
this gradient is used to calculate the search direction
during a conjugate gradient step [42]. The
is the weight associated with each grid point.
Here a contravariant-to-covariant
tensor correction is needed when
this gradient is used to calculate the search direction
during a conjugate gradient step [42]. The
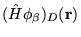 functions in general
contain contributions from all delta functions
of the simulation cell but we wish to keep
functions in general
contain contributions from all delta functions
of the simulation cell but we wish to keep
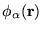 restricted to its spherical region.
For this reason in every minimisation step of
(21) we zero all the components
of (24) that correspond to delta
functions outside the sphere of
restricted to its spherical region.
For this reason in every minimisation step of
(21) we zero all the components
of (24) that correspond to delta
functions outside the sphere of
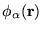 .
.
When the minimisation with respect to the density
kernel of equation (22) is carried out
under the electron number and idempotency constaints,
equation (24) contains extra terms
as a result of the constraints imposed in
(22). These terms ensure that the
electron number and idempotency constraints are
automatically obeyed in (21) and as
a result, the optimisation with respect to the
support functions can be carried out in an
unconstrained fashion.


Next: The FFT box technique
Up: Nonorthogonal generalized Wannier function
Previous: Charge density and total
Peter D. Haynes
2002-10-31
![]() . From equation (10) we see that
the charge density is expanded in fine grid delta functions where
. From equation (10) we see that
the charge density is expanded in fine grid delta functions where
![]() are the expansion coefficients. Therefore the energy will
have a variational dependence on these coefficients
provided they form an
are the expansion coefficients. Therefore the energy will
have a variational dependence on these coefficients
provided they form an ![]() -representable charge density.
Consequently, the energy should also have a variational dependence
on the density kernel
-representable charge density.
Consequently, the energy should also have a variational dependence
on the density kernel
![]() and the
NGWF expansion coefficients
and the
NGWF expansion coefficients
![]() since the
since the
![]() are constructed from them
are constructed from them