The FFT box

Linear-scaling can be achieved by restricting the number of plane waves that each basis function is comprised of so that it is independent of system-size. In other words, because the NGWFs are strictly zero outside their respective localisation regions, we need not use the entire simulation cell to perform FFTs on them, but may use a much smaller region. This must be done in such a way as to preserve the Hermiticity of operators, i.e. so that

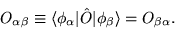$$O_{\alpha\beta} \equiv \langle\phi_{\alpha}\vert\hat{O}\vert\phi_{\beta}\rangle = O_{\beta\alpha}.$$ (19)

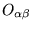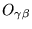Also, it is important that the representation of an operator in this new, contracted basis is consistent throughout the calculation: when we compute the two matrix elements $O_{\alpha\beta}$ and $O_{\gamma\beta}$, in both cases we require the quantity 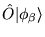$\hat{O}\vert\phi_{\beta}\rangle$, and in both cases this quantity should be the same.

We investigated these matters in detail in the context of the kinetic energy in an earlier communication [18], and we found an efficient and accurate solution that we call the `FFT box' technique, which involves perfoming computations over restricted regions of the simulation cell, using the fact that the NGWFs are localised in real space. First we shall define the FFT box and then show in detail how it is used to compute the matrix elements of each component of the Hamiltonian in 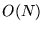$O(N)$ operations.

Figure 2: The simulation cell and FFT box for a pair of overlapping NGWFs, 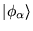$\vert\phi_{\alpha}\rangle$ and $\vert\phi_{\beta}\rangle$

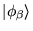
We define the FFT box to be a miniature and commensurate version of the simulation cell whose size is such that it can contain any pair of NGWFs that exhibit any degree of overlap. Its dimensions and shape are determined at the start of a calculation and are universal throughout that calculation. It should have the same spacing of grid points in each lattice vector direction as the simulation cell, and its origin (which is in general different for the calculation of each matrix element) should coincide with a particular grid point of the simulation cell (Figure 2). Treating the FFT box as a miniature simulation cell with 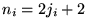$n_{i} = 2j_{i} + 2$ points along lattice vector 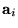$\mathbf{a}_{i}$ (where the 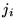$j_{i}$ are integers), and with volume 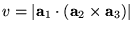$v = \vert \mathbf{a}_{1} \cdot (\mathbf{a}_{2} \times \mathbf{a}_{3}) \vert$, we may define a set of basis functions, 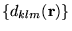$\{ d_{klm}(\mathbf{r}) \}$, as we did for the whole simulation cell in equation (1), as follows,

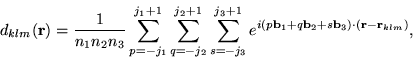$$d_{klm}(\mathbf{r}) = \frac{1}{n_{1}n_{2}n_{3}} \sum_{p=-j_{... ...f{b}_{2}+s\mathbf{b}_{3})\cdot (\mathbf{r}-\mathbf{r}_{klm})},$$ (20)

where the sum runs over the reciprocal lattice vectors, 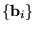$\{ \mathbf{b}_{i} \}$, of the FFT box (i.e., a number of plane-waves that is now independent of system size), and

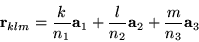$$\mathbf{r}_{klm} = \frac{k}{n_{1}}\mathbf{a}_{1} + \frac{l}{n_{2}}\mathbf{a}_{2} + \frac{m}{n_{3}}\mathbf{a}_{3}$$ (21)

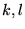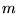for integer $k,l$, and $m$. These basis functions have the periodicity of the FFT box, and all the analytic properties derived for the basis functions of the simulation cell in Appendix A carry over to these functions by making the replacements

$$V \longrightarrow v$$

$$N_{i} \longrightarrow n_{i}$$

$$\mathbf{A}_{i} \longrightarrow \mathbf{a}_{i}$$

$$\mathbf{B}_{i} \longrightarrow \mathbf{b}_{i}$$

$$D_{KLM}(\mathbf{r}) \longrightarrow d_{klm}(\mathbf{r})$$

$$B_{XYZ}(\mathbf{r}) \longrightarrow b_{xyz}(\mathbf{r}).$$ (22)