

Next: Kinetic energy
Up: Total energy using the
Previous: The FFT box
We must also introduce an operator,
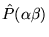 , that is required to project NGWFs between their representation in terms of the plane-waves of the entire simulation cell and those of the FFT box. This operator has arguments
, that is required to project NGWFs between their representation in terms of the plane-waves of the entire simulation cell and those of the FFT box. This operator has arguments 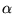 and
and 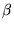 as it is dependent upon the exact location of the FFT box within the simulation cell, which in turn depends upon the particular matrix element that is being calculated. We thus define for the pair of NGWFs
as it is dependent upon the exact location of the FFT box within the simulation cell, which in turn depends upon the particular matrix element that is being calculated. We thus define for the pair of NGWFs 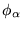 and
and 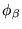 :
:
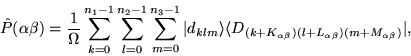 |
(23) |
where
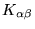 ,
,
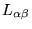 and
and
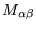 are integers denoting the grid point of the simulation cell at which the origin of the FFT box (
are integers denoting the grid point of the simulation cell at which the origin of the FFT box (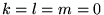 ) is located, and
) is located, and 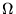 is the volume per grid point.
is the volume per grid point.
When this operator acts upon a function with the periodicity of the simulation cell, i.e., a function given by equation (3), it maps it onto the `same' function with the periodicity of the FFT box:
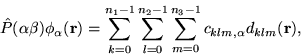 |
(24) |
where
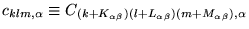 .
.
Similarly, we define a supplementary operator,
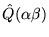 , that performs the same task, but for the fine grid representation:
, that performs the same task, but for the fine grid representation:
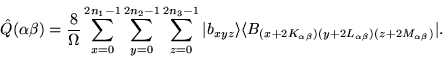 |
(25) |
The operators
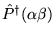 and
and
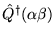 map functions from the FFT box back to the simulation cell on the standard and fine grids respectively.
map functions from the FFT box back to the simulation cell on the standard and fine grids respectively.


Next: Kinetic energy
Up: Total energy using the
Previous: The FFT box
Peter D. Haynes
2002-10-29
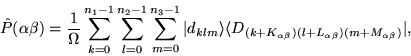
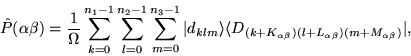
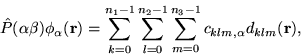
![]() , that performs the same task, but for the fine grid representation:
, that performs the same task, but for the fine grid representation:
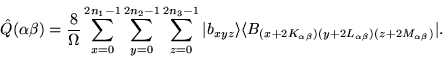
![]() and
and
![]() map functions from the FFT box back to the simulation cell on the standard and fine grids respectively.
map functions from the FFT box back to the simulation cell on the standard and fine grids respectively.