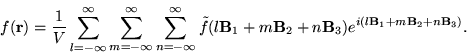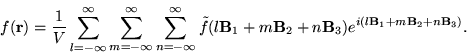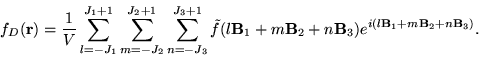

Next: Basis for the fine
Up: Basis Set
Previous: Localisation and Orthogonality
Consider a cell periodic function, 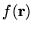 , which may be written in terms of its discrete Fourier series
, which may be written in terms of its discrete Fourier series
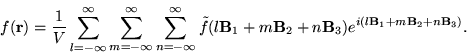 |
(50) |
Consider also the bandwidth limited version of this same function,
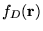 , which has only the same frequency components as
, which has only the same frequency components as 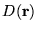 :
:
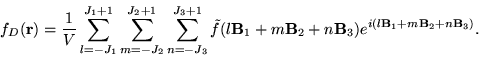 |
(51) |
It can be shown that the projection of 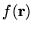 onto a particular basis function is exactly equal to that of
onto a particular basis function is exactly equal to that of
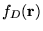 , and that furthermore, replacing the integral by a discrete sum over grid points leads to exactly the same answer:
, and that furthermore, replacing the integral by a discrete sum over grid points leads to exactly the same answer:
This result is very useful for our purposes as it tells us that the overlap integral of any cell periodic function with a function that is represented by our basis set, can be evaluated exactly as a summation over grid points.


Next: Basis for the fine
Up: Basis Set
Previous: Localisation and Orthogonality
Peter D. Haynes
2002-10-29