Localisation and Orthogonality

Each basis function is localised on the grid, i.e., its value is unity at the grid point at which it is centered and zero on all other grid points of the simulation cell:

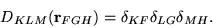$$D_{KLM}(\mathbf{r}_{FGH}) = \delta_{KF}\delta_{LG}\delta_{MH}.$$ (48)

Furthermore, basis functions centered on different sites are orthogonal:

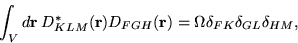$$\int_{V} d\mathbf{r} \: D_{KLM}^{\ast}(\mathbf{r}) D_{FGH}(\mathbf{r}) = \Omega \delta_{FK}\delta_{GL}\delta_{HM},$$ (49)

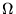where $\Omega$ is the volume per grid point of the standard grid.