
Next: Conclusions
Up: Total-energy calculations on a
Previous: Total energy optimisation
Results and discussion
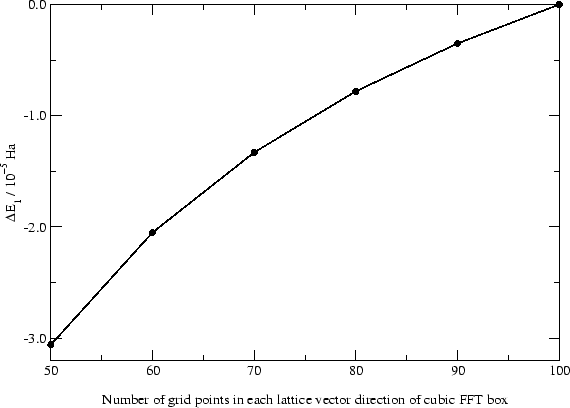
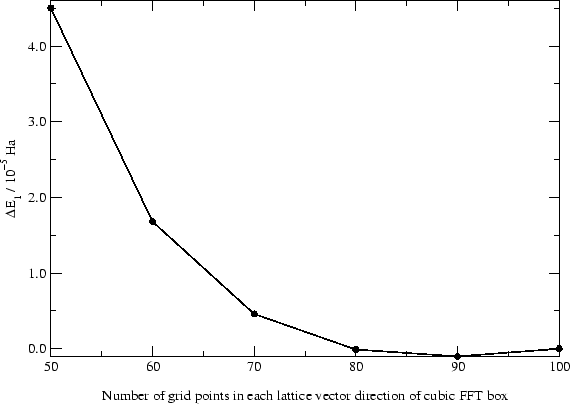
We now present some results of calculations we have performed using the methods described above. We first demonstrate the accuracy of the FFT box technique as compared to using the entire simulation cell as the FFT grid. Figure 4 shows the quantity 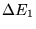 , defined as
, defined as
![\begin{displaymath}
\Delta E_{1} \equiv E^{\mathrm{box}}[n] - E[n],
\end{displaymath}](img203.png) |
(46) |
for the molecules silane (
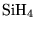 ) and cyclohexane (
) and cyclohexane (
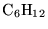 ), for different FFT box sizes. For these tests we used a cubic simulation cell of side length
), for different FFT box sizes. For these tests we used a cubic simulation cell of side length 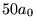 , although any other lattice symmetry could easily have been employed. The PAOs are confined within spherical regions of radius
, although any other lattice symmetry could easily have been employed. The PAOs are confined within spherical regions of radius 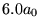 , and vanish exactly at the region boundary [20]. They were generated using norm-conserving pseudopotentials [26], the local density approximation (LDA), and an energy cut-off of 538 eV (corresponding to our grid spacing of
, and vanish exactly at the region boundary [20]. They were generated using norm-conserving pseudopotentials [26], the local density approximation (LDA), and an energy cut-off of 538 eV (corresponding to our grid spacing of 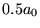 ). In the case of silane the silicon atom had one 3s and three 3p PAOs, and for cyclohexane the carbon atoms had one 2s and three 2p PAOs. The hydrogen atoms all had a single 1s PAO.
). In the case of silane the silicon atom had one 3s and three 3p PAOs, and for cyclohexane the carbon atoms had one 2s and three 2p PAOs. The hydrogen atoms all had a single 1s PAO.
Figure 4:
Top panel: 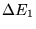 plotted for a silane molecule as a function of FFT box size. Bottom panel: the same quantity plotted for cyclohexane. In both cases all PAOs were confined to atom centered localisation regions with radius
plotted for a silane molecule as a function of FFT box size. Bottom panel: the same quantity plotted for cyclohexane. In both cases all PAOs were confined to atom centered localisation regions with radius 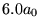 , and the grid spacing was
, and the grid spacing was 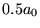 .
.
|
|
We see that the error associated with the FFT box technique are of the order of a few
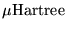 per atom, which is comparable to the inherent errors present in plane-wave DFT. We note that the convergence of the total energy with FFT box size is not expected to be variational, and indeed it is not: the FFT box technique should be viewed as a good approximation to the `correct' result that would be obtained by using the entire simulation cell to perform FFTs for calculating the total energy. For a given FFT box size, however, the kinetic energy cut-off of our basis functions (and hence the grid spacing) is a variational parameter, just as in traditional plane-wave DFT.
per atom, which is comparable to the inherent errors present in plane-wave DFT. We note that the convergence of the total energy with FFT box size is not expected to be variational, and indeed it is not: the FFT box technique should be viewed as a good approximation to the `correct' result that would be obtained by using the entire simulation cell to perform FFTs for calculating the total energy. For a given FFT box size, however, the kinetic energy cut-off of our basis functions (and hence the grid spacing) is a variational parameter, just as in traditional plane-wave DFT.
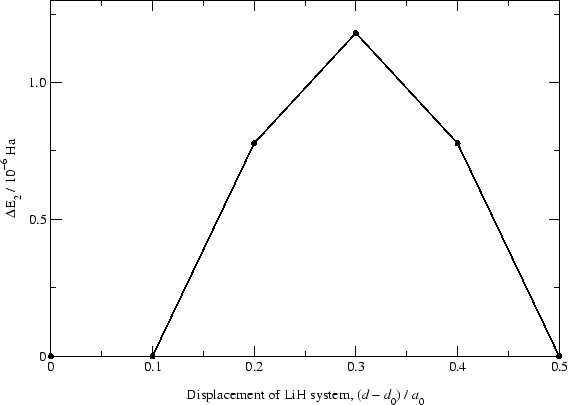
In addition, we look at a feature common to all real space grid methods, namely the variation of the energy as the system is translated by fractions of a grid spacing with respect to the simulation cell. We define the quantity 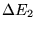 to be
to be
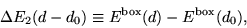 |
(47) |
where 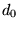 is a reference position of the system, and
is a reference position of the system, and 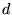 is some
rigid displacement with respect to the grid. The top panel in Figure
5 shows this variation, in steps of
is some
rigid displacement with respect to the grid. The top panel in Figure
5 shows this variation, in steps of 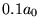 , for a
lithium hydride (LiH) molecule on a cubic grid with grid spacing
, for a
lithium hydride (LiH) molecule on a cubic grid with grid spacing 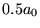 . The PAOs of both lithium and hydrogen had localisation radii
of
. The PAOs of both lithium and hydrogen had localisation radii
of 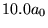 , and were generated in the same way as described
above.
, and were generated in the same way as described
above. 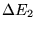 can be seen to be of the order of
can be seen to be of the order of
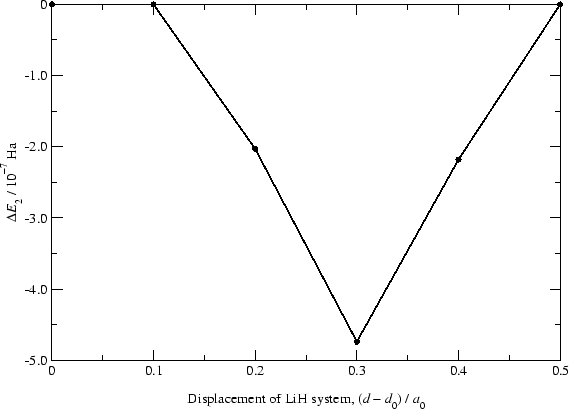
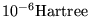 . The bottom panel shows the same quantity, but this
time with optimisation of the NGWF coefficients,
. The bottom panel shows the same quantity, but this
time with optimisation of the NGWF coefficients,
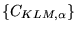 , in addition to the elements of the density kernel
[27]. We see that the variation in total energy is
reduced to the
, in addition to the elements of the density kernel
[27]. We see that the variation in total energy is
reduced to the
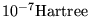 level. We expect the
optimisation of the NGWF coefficients to be important for performing
accurate geometry optimisations.
level. We expect the
optimisation of the NGWF coefficients to be important for performing
accurate geometry optimisations.
Figure 5:
Top panel: Variation in total energy, 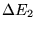 , as the LiH molecule is translated by fractions of a grid spacing. The PAOs on both the lithium and hydrogen atoms had a radius of
, as the LiH molecule is translated by fractions of a grid spacing. The PAOs on both the lithium and hydrogen atoms had a radius of 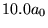 . Bottom panel: The same quantity, but with optimisation of the PAO coefficients [27].
. Bottom panel: The same quantity, but with optimisation of the PAO coefficients [27].
|
|


Next: Conclusions
Up: Total-energy calculations on a
Previous: Total energy optimisation
Peter D. Haynes
2002-10-29
![]() per atom, which is comparable to the inherent errors present in plane-wave DFT. We note that the convergence of the total energy with FFT box size is not expected to be variational, and indeed it is not: the FFT box technique should be viewed as a good approximation to the `correct' result that would be obtained by using the entire simulation cell to perform FFTs for calculating the total energy. For a given FFT box size, however, the kinetic energy cut-off of our basis functions (and hence the grid spacing) is a variational parameter, just as in traditional plane-wave DFT.
per atom, which is comparable to the inherent errors present in plane-wave DFT. We note that the convergence of the total energy with FFT box size is not expected to be variational, and indeed it is not: the FFT box technique should be viewed as a good approximation to the `correct' result that would be obtained by using the entire simulation cell to perform FFTs for calculating the total energy. For a given FFT box size, however, the kinetic energy cut-off of our basis functions (and hence the grid spacing) is a variational parameter, just as in traditional plane-wave DFT.
![]() to be
to be