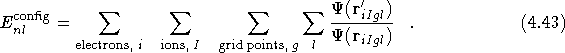
If the non-local energy is strongly coupled to the expectation values of other observables via the trial/guiding wavefunction, then even though the non-local potential energy itself is a small fraction of the total energy, it is necessary to include it in the variance minimisation procedure. This can be achieved by storing all the information required to evaluate the change in the ratio of the wavefunction as the variational parameters change, at each of the grid points on which the original value of the non-local energy is stored. Schematically, one can write the total non-local energy for a single configuration as
All the other electrons in the ratio
have been dropped from the
notation and are assumed to be kept fixed. Eq.(
) can
be simplified by using the fact that the non-local pseudopotential is
relatively short ranged. Each electron only feels the effect of the
non-local pseudopotential from one or two ions. The first two
summations can therefore be replaced with a summation over
hits. A hit is the event where an electron in the configuration
is close enough to an ion to feel the effect of its non-local
pseudopotential:
In a similar approach to that of Eq.() the contribution
to the ratio for each grid
point of each hit in each configuration from the function, u
function and determinant are stored at the start of the
optimisation procedure. For example, the contribution to each ratio of
functions can summed over all the 
vectors in each star, s,
such that
The ratio of the function at the points 
and 
can then be quickly reconstructed for each set of trial parameters
from
A similar method of storage is adopted for the u function and the Slater determinant.
