As the expectation value of the non-local pseudopotential taken with
respect to the trial wavefunction is a small fraction of the total
energy,
one option is to store the non-local energy associated with each
configuration at the beginning of the optimisation procedure and keep
it fixed. Care has to be taken when adopting this method to be sure
to evaluate the non-local energy to sufficient accuracy at the
beginning of the optimisation procedure. During a VMC calculation,
the non-local pseudopotential is evaluated by the method proposed by
Fahy et al. [26]. The non-local Hamiltonian for the i 
electron is given by
where the ion is at the origin. 
is the angular momentum l
projection operator acting at a distance r from the origin;
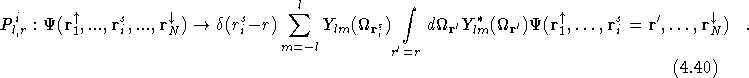
The non-local energy is then evaluated along the Monte Carlo random
walk of points sampled from 
according to
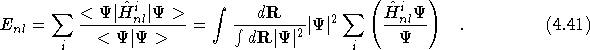
The z-axis is chosen along 
to use the fact that
for 
to simplify
such that
The integral over 
in Eq.(
) is performed
statistically with the QMC code. A series of points are sampled on a
grid surrounding each ion and the ratio of the value of the
wavefunction with all other electrons fixed, and the 
electron
at 
and at each of the grid points is used to evaluate
Eq.().
During a VMC calculation, it is not necessary to sample enough points
from the spherical grid to evaluate the non-local integral to high
precision. Any variance in the value of Eq.() will
be averaged out over the duration of the run. However, if the
non-local energy is to be kept fixed throughout a variance
minimisation run, it is important to ensure the sampling in the
non-local integral is sufficient for each individual value of
the non-local energy to have a small variance. Typically, up to 8
times as many sampling points are used to ensure accurate individual
values of the non-local potential energy compared with a normal VMC
calculation.
