This approximation starts from the one-electron equations of
Eq(
). 
is chosen to try to model the
interaction terms in this equation. The ions contribute a potential
All the other electrons in the system also contribute to the
potential. The potential due to the electrons is approximated by the
electrostatic interaction with all the others, which can be written in
terms of the electron density, 
, as
where the self-interaction potential due to electron i has been removed.
To actually calculate the Hartree potential it is necessary to know
the electronic charge distribution of the system. If the electrons are
assumed to be independent of each other, then it is straightforward to
construct from the single electron eigenstates
where the summation over i includes all occupied states. Using this charge density the total one-electron potential is
The potential 
is different for each orbital, and
therefore the orbitals are not orthogonal. Note that
depends on all the other orbitals, 
, and so the solution
of Eq.() must be found self-consistently.
The choice of in Eq.() all seems a bit
like guesswork, but it can also be derived using the variational
principle. We start with Eq.(). The electrons
are assumed to be non-interacting, and so the N-electron wavefunction
is just the product of the one-electron wavefunctions,
This 
can be used with Eq.() to find the expectation
value of 
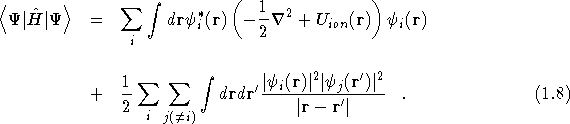
Introducing a Lagrange multiplier, 
, for the condition
that the one-electron wavefunctions are normalised, and minimising
the above equation with respect to the wavefunctions, so that
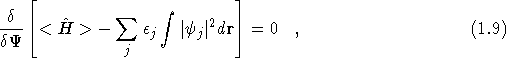
leads to a set of single particle equations,
which are the same as substituting Eq.() in
Eq.(). These equations are known as the Hartree
equations.
