The Hartree-Fock approximation is an extension of the above Hartree approximation to include the permutation symmetry of the wavefunction which leads to the exchange interaction. Exchange is due to the Pauli exclusion principle, which states that the total wavefunction for the system must be antisymmetric under particle exchange. This means that when two arguments are swapped the wavefunction changes sign as follows:
where 
includes coordinates of position and spin. Therefore
no two electrons can have the same set of quantum numbers, and
electrons with the same spin cannot occupy the same state
simultaneously.
Instead of using the simple product form of the wavefunction shown in
Eq.(
), a Slater determinant
wavefunction[5, 6] which satisfies antisymmetry is
used
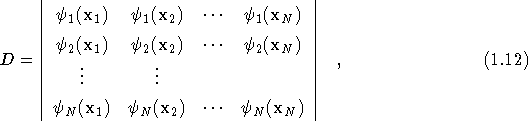
where 
are the one-electron wavefunctions.
Following exactly the same method of minimising the expectation value
of 
with respect to the one-electron wavefunctions as was
used in the derivation of the Hartree equations, results in the
following set of one-electron equations, the Hartree-Fock equations;
where 
labels the spin of particle i. Note the
self-interaction cancels out from the second and third terms. The
extra term in these equations, when compared to
Eq.(), is known as the exchange term and is only
non-zero when considering electrons of the same spin. The effect of
exchange on the many-body system is that electrons of like spin tend
to avoid each other. As a result of this, each electron has a ``hole''
associated with it which is known as the exchange hole (or the Fermi
hole). This is a small volume around the electron which like-spin
electrons avoid. The charge contained in the exchange hole is positive
and exactly equivalent to the absence of one-electron.
Unlike all the other terms acting on 
, the exchange term is a
non-local integral operator and this makes the Hartree-Fock equations
hard to solve in all but a few special cases.
