Choice of Functional Form for new term in the Jastrow Factor

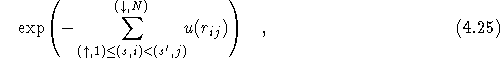
In the case of optimising , the choice of parameters to optimise was obvious as the function is expressed as a Fourier expansion. In the case of the Jastrow function, this choice is not so clear. The current Jastrow factor has the form

 

where is given by

 

In an attempt to improve on the above function it was decided to add an extra term into the exponential in Eq.() to take account not only of the electron-electron separation, , but also of the individual positions of the electrons and . It was suspected that the region where correlation effects are likely to deviate most strongly from the symmetric correlation described by the standard Jastrow function will be close to the ionic cores. Therefore, the any new function, should be short ranged and centred on each of the ions. For simplicity, the function was chosen to be a function of the distances of the 2 electrons from the ion, and and the electron-electron separation , with no angular dependence. It must also obey the following conditions:-

1. It should not cause the total Jastrow term to violate the cusp condition (see section ), i.e. for the extra term .  
2. should be well behaved as one of the electrons moves through an ion, i.e. there should be no cusp in or in the 1st derivative as . 
3. should take the most general form possible, subject to the above 2 restrictions.

To check that condition was satisfied, the new term, was expanded about

Now condition specifies , therefore

 

Finally, expanding gives

We chose to keep electron j fixed (i.e. ) and move electron i through it, to test the behaviour as . As the angle between and varies between 0 and the value of will vary smoothly between -1 and +1, (see figure ).

  
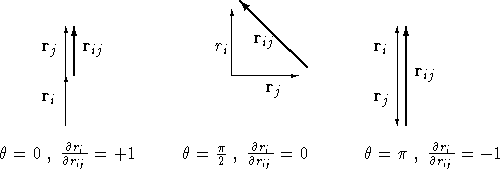
Figure: Dependence of on the angle between and

Therefore, the only solution to Eq.() for all geometries of electrons is .

The final form chosen for the new short range function was therefore

 

The prefactor in Eq.() performs the following functions; the term removes any terms independent of or terms linear in as specified above. The term is required to satisfy condition , namely that the function be well behaved as one of the electrons moves through the ion. The need for this term in the prefactor was established by performing small simulations using different forms of as one electron moves through an ion. The term enforces the short range nature of by forcing it to decay to zero with zero gradient when one of the electrons is a distance L from the ion. The remaining part of is a general Chebyshev expansion in all three variables; , and .

It should be noted that there are in fact two separate functions required, one dealing with the case where the spins of electrons i and j are parallel and one where they are anti-parallel. This has no effect on the choice of functional form, but it does mean that there are twice as many parameters to be optimised and this reduces the maximum possible number of terms in the Chebyshev expansion.

It is also worth noting that the final form for is very similar to that proposed by Mitas [41], see Eq.(). The difference between the functions is that Mitas only includes even powers of whereas the function used here contains odd and even powers and should therefore be more general.