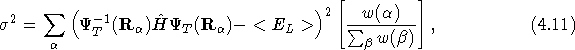
We begin by writing the variance of the energy as
where 
is the Hamiltonian as defined in chapter 
and 
is the trial/guiding wavefunction which is to be
optimised. The sum is over a set of 3N-dimensional electron
configurations, 
, 
is an average energy,
and the reweighting factors, 
, are given by
The electron configurations are sampled from the starting distribution
and then kept fixed throughout the optimisation. This
``correlated sampling'' approach gives a good estimate of the
difference in variance between wavefunctions corresponding to
different sets of parameters. The process can be used iteratively by
using the optimised set of parameters to regenerate a new set of
configurations which are then used to perform a new optimisation. This
is useful when the reweighting factors differ significantly from unity
(see section ). The non-linear optimisations over the
multi-dimensional parameter spaces were performed using the NAG\
routine E04FCF. This works by finding the unconstrained minimum of a
sum of squares, as in Eq.(), using a modified Newton
algorithm that requires the function values only.
