The general Hamiltonian of Eq.(
) can be adapted for
a supercell calculation in the following way
where 
is the set of translation vectors of the supercell
lattice, the potential 
has the periodicity of
, and N is the number of electrons in the supercell. In
the case where the supercell is constructed from integer multiples of
the primitive unit cells, as is the case for all the calculations
described here, also then has the periodicity of the set
of translation vectors of the underlying crystal lattice.
Trial wavefunctions for this supercell Hamiltonian are based on the
general trial wavefunction introduced in Eq.(),
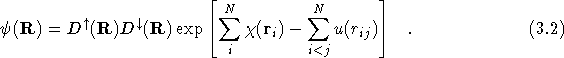
The Slater determinants are constructed from one-electron orbitals
obtained from an LDA calculation. The 
-point sampling in the
LDA calculation is chosen to produce the desired number of
one-electron orbitals for constructing the Slater determinant in the
QMC trial/guiding wavefunction. For example, if an n=1, 1x1x1
supercell is chosen for the QMC calculation then the LDA calculation
is also performed on a single unit cell and the wavefunctions are
sampled at one -point. If an n=2, 2x2x2 supercell is
chosen for the QMC calculation then the LDA calculation is again
performed on a single unit cell but now the wavefunctions are sampled
from a 2x2x2 mesh of -points in the Brillouin Zone of the
primitive lattice.
Recently, new insights have been made into the best choice for the
-points at which the one-electron wavefunctions should be
calculated
[33, 50] for use in QMC calculations. To
understand these, first one should consider the translational
symmetries of the above Hamiltonian.
is invariant under the translation of any electron
coordinate by a vector in . is invariant under the simultaneous translation of all electron
coordinates by a vector in .
Symmetry (1) implies that the wavefunction can only change by a phase
factor when any single electron is translated by a supercell lattice
vector. The indistinguishability of the electrons ensures that this
phase factor must be the same no matter which electron is moved. This
can be demonstrated by applying Bloch's theorem separately to the
first and second arguments of the wavefunction and, for the moment,
assuming that the two -vectors are different;
We can then apply the permutation symmetry to Eq.():
We now translate the second argument by 
,
and then apply permutation symmetry once more, giving
It therefore follows that
where 
is the set of vectors reciprocal to .
The vectors 
and 
can be reduced into the first
Brillouin Zone (BZ) of the supercell reciprocal lattice, therefore we
can choose 
without loss on generality.
The wavefunction can therefore be written in the form
where 
is invariant under the translation
of any electron coordinate by a vector in , and is
antisymmetric under particle exchange.
Now consider the second symmetry of which states that the
wavefunction can only change by a phase factor when all the electrons
are translated by a vector in . This allows us to write
where 
is the crystal momentum of the wavefunction and
can be reduced into the first BZ of the lattice reciprocal
to . It therefore follows that 
can be written in
the alternative form
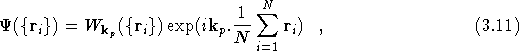
where 
in invariant under the simultaneous translation
of all electron coordinates by a vector in and is
antisymmetric under particle exchange.
The operators which translate all the electrons by a vector in
and the operators which translate a single electrons
by a vector in commute with each other and with the
Hamiltonian, i.e. they form a complete set of commuting operators.
Therefore the eigenfunctions of the Hamiltonian in
Eq.() can be chosen to satisfy both the
above symmetries at the same time. We can obtain a relationship
between the values of and 
by translating all
the electrons by a vector in (which is a subset of
), and using Eq.() we find
This must agree with Eq.(), which yields
In a QMC trial wavefunction, the value of is determined by
the Slater determinant. If all the one-electron wavefunctions making
up the determinant reduce to the same value of in the
supercell BZ, then the overall determinant and hence the wavefunction
will have that value of . The value of for a
QMC trial wavefunction is determined by the sum of all the
values of the one-electron wavefunctions making up the determinant.
Applications of QMC prior to Refs.[33, 50] used
the conceptually simplest choice of and ,
namely 
. This is achieved by choosing the -values for the one-electron orbitals on a uniform grid or mesh centred on the origin in
reciprocal space, with a grid spacing 
.
In the limit of an infinite simulation cell, the value of
must tend to zero. However, for a finite simulation cell, the
groundstate does not always take the values
[33]. In the following section,
we consider the specific systems of diamond structure germanium and
silicon and explore what is the best choice of values of
and for these systems.
