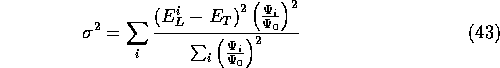



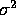 .
.
The 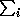 in Equ. (
in Equ. ( ) is a sum over a set of configurations i,
where
) is a sum over a set of configurations i,
where 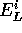 is the local energy of configuration i when evaluated
with the current set of trial parameters (see section
is the local energy of configuration i when evaluated
with the current set of trial parameters (see section  ).
).
The main advantage of the optimisation technique ( ) is
that it incorporates the use of correlated sampling. i.e. the same set
of configurations i is used to evaluate (
) is
that it incorporates the use of correlated sampling. i.e. the same set
of configurations i is used to evaluate ( ) for each set of
trial parameters during the optimisation procedure. This introduces a
significant cancellation of errors which makes the whole scheme feasible.
It may appear slightly contrary to intuition that
the best way to optimise
) for each set of
trial parameters during the optimisation procedure. This introduces a
significant cancellation of errors which makes the whole scheme feasible.
It may appear slightly contrary to intuition that
the best way to optimise 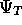 is using (
is using ( )
and not just to minimise the energy.
If one optimises the energy directly, the wavefunction
produced has an associated energy that is not very smooth,
instead it contains small regions of
space where the energy is very much lower than average.
This does indeed lower the
overall energy in the optimisation procedure, but it doesn't produce
a wavefunction which is closer
to the true groundstate wavefunction.
If a VMC calculation is performed using the parameters obtained from
minimising the energy of a given wavefunction, the final value for the
energy obtained from the VMC calculation is usually considerably higher
than the final value obtained from the optimisation scheme. This is in
direct contrast to the results obtained from VMC calculations performed
using wavefunctions obtained from minimising the variance of the energy
of a given wavefunction, where the energy did not rise significantly (
see section
)
and not just to minimise the energy.
If one optimises the energy directly, the wavefunction
produced has an associated energy that is not very smooth,
instead it contains small regions of
space where the energy is very much lower than average.
This does indeed lower the
overall energy in the optimisation procedure, but it doesn't produce
a wavefunction which is closer
to the true groundstate wavefunction.
If a VMC calculation is performed using the parameters obtained from
minimising the energy of a given wavefunction, the final value for the
energy obtained from the VMC calculation is usually considerably higher
than the final value obtained from the optimisation scheme. This is in
direct contrast to the results obtained from VMC calculations performed
using wavefunctions obtained from minimising the variance of the energy
of a given wavefunction, where the energy did not rise significantly (
see section  ).
).
A more subtle problem is the choice of 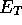 in Eqn.(
in Eqn.( ) which
can be calculated by three different methods. These can in some way
be viewed as a logical progression where
) which
can be calculated by three different methods. These can in some way
be viewed as a logical progression where 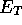 changes more and
more frequently.
changes more and
more frequently.
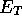 to be the best energy achieved from a VMC calculation using the original parameters.
to be the best energy achieved from a VMC calculation using the original parameters.
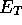 in this way and performed an
optimisation as in Eqn.(
in this way and performed an
optimisation as in Eqn.( ).
He then recalculated a new set of configurations by performing a VMC
calculation with the optimised parameters. He then took the energy from
that calculation to be the new
).
He then recalculated a new set of configurations by performing a VMC
calculation with the optimised parameters. He then took the energy from
that calculation to be the new 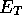 and repeated the whole process.
He usually performed 3 or 4 iterations to reach a converged set of optimised
parameters.
and repeated the whole process.
He usually performed 3 or 4 iterations to reach a converged set of optimised
parameters.
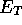 more frequently than Umrigar by setting
more frequently than Umrigar by setting
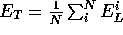 . With this method, the function being
optimised is now a much more complicated function of the trial parameters
but the computer is obviously oblivious to this!
Again, one could in principle iterate this technique, just as in the one
above but this does not prove to be necessary.
. With this method, the function being
optimised is now a much more complicated function of the trial parameters
but the computer is obviously oblivious to this!
Again, one could in principle iterate this technique, just as in the one
above but this does not prove to be necessary.
All three of the above methods were experimented with by optimising the function for a germanium atom. Method  produced the
poorest results as might be expected, because as soon as the parameters
change, one is minimising the variance about an energy which is quite
different to the true mean energy of the configurations.
Method
produced the
poorest results as might be expected, because as soon as the parameters
change, one is minimising the variance about an energy which is quite
different to the true mean energy of the configurations.
Method  produced good results, but does
need several iterations of the optimisation routine to produce a
converged result.
Method
produced good results, but does
need several iterations of the optimisation routine to produce a
converged result.
Method  produced results comparable with method
produced results comparable with method
 , but does not require multiple calls to the
optimisation routine.
When optimising the function for solid germanium, the extra VMC
calculations required to make multiple iterations of the optimisation routine
become very computationally expensive and so the only practical method is no.
, but does not require multiple calls to the
optimisation routine.
When optimising the function for solid germanium, the extra VMC
calculations required to make multiple iterations of the optimisation routine
become very computationally expensive and so the only practical method is no.
 .
.


