As stated in section 
, the many body wavefunction can be
written in the following form.
The wavefunction in () is normally referred to as the
Hartree-Fock Jastrow Chi wavefunction. All three parts of the
wavefunction i.e. the HF determinant, Jastrow factor and Chi function
would benefit from some form of optimisation of parameters, and so
deciding which part to optimise is a matter of deciding which part
should yield the greatest improvement in the quality of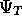 
when optimised.
The Chi function has previously been constructed according to a scheme
introduced by Fahy [9], using Eqn.(). Of the
three parts of the Hartree-Fock-Jastrow-Chi trial wavefunction, this function has the weakest theoretical justification for its form.
It is constructed on an ad hoc basis by saying that the LDA charge
density is assumed to be reasonably close to the real charge density
and so by constructing as in () this should also
produce a charge density close to the experimental value.
where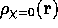 
is the density produced
by a VMC calculation using a trial wavefunction,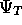 
with ¸=0.
Equation () certainly does produce a that is
able to reduce the energy of the system (compared to a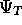 
with
¸ =0, see Figure ) and produce a charge density that
is a reasonable reflection of the LDA charge density
(see Figure ). However, there is nothing to suggest that a function constructed using () is the best possible function
either in terms of total energy or charge density.
Indeed, there is no hard evidence [10] of exactly
how accurate the LDA charge density is.
It therefore seemed sensible to start optimising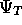 
by optimising ¸.
Figure: Charge Density along the Ge-Ge bond for different functions.
