Calculating elastic constants

The CASTEP Elastic Constants task return results as a group of .castep output files. Each of them represents a geometry optimization run with a fixed cell, for a given strain pattern and strain amplitude. The naming convention for these files is:

seedname_cij__m__n

Where m is the current strain pattern and n is the current strain amplitude for the given pattern.

You can then use CASTEP to analyze the calculated stress tensors for each of these runs and generate a file with information about elastic properties. The information in this file includes:

A summary of the input strains and calculated stresses.
Results of linear fitting for each strain pattern, including the quality of the fit.
The correspondence between calculated stresses and elastic constants for a given symmetry.
A table of elastic constants, C_ij, and elastic compliances, S_ij.
The derived properties such as bulk modulus and its inverse, compressibility, Young modulus and Poisson ratios for three directions, and the Lamé constants required for modeling the material as an isotropic medium.

If you requested the polarization property, the main output file, seedname.castep, contains the piezoelectric tensor output at the end, for example:

       Symmetrized Piezoelectric Stress Tensor (C/m^2)
       -----------------------------------------------
  0.000000   0.000000   0.000000   0.000000  -0.918444   0.000000
  0.000000   0.000000   0.000000  -0.918444   0.000000   0.000000
 -0.600778  -0.600778   1.321444   0.000000   0.000000   0.000000

To calculate elastic constants

From the Materials Studio menu bar, select Modules | CASTEP | Analysis.
From the list of properties, select Elastic constants.
Use the Results file selector to pick the appropriate results file.
Click Calculate.
This creates a new text document, seedname Elastic Constants.txt, in the results folder.

Description of the elastic constants file

Here, the example of a tetragonal rutile crystal, TiO₂, illustrates the contents of the Elastic Constants.txt output file produced by CASTEP.

This lattice type requires two strain patterns. For each strain pattern, there is a summary of the calculated stresses as extracted from the respective .castep files:

         Summary of the calculated stresses
         **********************************
 
Strain pattern:      1
======================
 
Current amplitude: 1
Transformed stress tensor (GPa) :
	 0.719908       -0.000000       -0.000000
	-0.000000        0.331220        0.369780
	-0.000000        0.369780        0.174538
 
Current amplitude: 2
Transformed stress tensor (GPa) :
 	 0.115598       -0.000000       -0.000000
	-0.000000       -0.019103        0.146509
	-0.000000        0.146509       -0.144727
						....

This provides information about the connection between components of the stress, strain, and elastic constants tensors. At this stage, each elastic constant's representation is a single compact index rather than by a pair of ij indices. Later, the file provides the correspondence between the compact notation and the conventional indexing:

 Stress corresponds to elastic coefficients (compact notation):
   1  7  8  4  0  11  
 
 as induced by the strain components:
   1  1  1  4  0  1

A linear fit of the stress-strain relationship for each component of the stress has the following format:

		       Stress    Cij       value of          value of
		       index    index       stress            strain
			1        1         0.719908         -0.003000
			1        1         0.115598         -0.001000
			1        1        -0.509448          0.001000
			1        1        -1.066455          0.003000
C (gradient)     :     299.206750
Error on C       :       4.882222
Correlation coeff:       0.999734
Stress intercept :      -0.185099

The gradient provides the value of the elastic constant (or a linear combination of elastic constants). The quality of the fit, indicated by the correlation coefficient, provides the statistical uncertainty of that value. The stress intercept value is not used in further analysis. It is an indication of how far the converged ground state was from the initial structure.

The output file then summarizes the results for all the strain patterns:

  ============================
  Summary of elastic constants
  ============================
 
 id  i  j       Cij (GPa)
 1   1  1     299.20675 +/-   4.882
 3   3  3     500.96355 +/-   2.004
 4   4  4     126.32975 +/-   4.509
 6   6  6     229.09375 +/-   0.826
 7   1  2     168.90265 +/-   4.411
 8   1  3     158.33975 +/-   4.590
 11   1  6       0.00000 +/-   0.000

This includes the errors only when the strain amplitude uses more than two values, since there is no statistical uncertainty associated with fitting a straight line to only two points.

The output files present the elastic constants in a conventional 6×6 tensor form, followed by a similar 6×6 representation of the compliances:

      =====================================
      Elastic Stiffness Constants Cij (GPa)
      =====================================
 
   299.20675   168.90265   158.33975     0.00000     0.00000     0.00000
   168.90265   299.20675   158.33975     0.00000     0.00000     0.00000
   158.33975   158.33975   500.96355     0.00000     0.00000     0.00000
     0.00000     0.00000     0.00000   126.32975     0.00000     0.00000
     0.00000     0.00000     0.00000     0.00000   126.32975     0.00000
     0.00000     0.00000     0.00000     0.00000     0.00000   229.09375
  
      ========================================
      Elastic Compliance Constants Sij (1/GPa)
      ========================================
 
   0.0051958  -0.0024785  -0.0008588   0.0000000   0.0000000   0.0000000
  -0.0024785   0.0051958  -0.0008588   0.0000000   0.0000000   0.0000000
  -0.0008588  -0.0008588   0.0025391   0.0000000   0.0000000   0.0000000
   0.0000000   0.0000000   0.0000000   0.0079158   0.0000000   0.0000000
   0.0000000   0.0000000   0.0000000   0.0000000   0.0079158   0.0000000
   0.0000000   0.0000000   0.0000000   0.0000000   0.0000000   0.0043650

The final part of the file contains the derived properties:

Bulk modulus              =    220.35108 +/-  2.572 (GPa)
 
Compressibility           =     0.00454 (1/GPa)

Elastic Debye temperature =   812.49749 K
Averaged sound velocity   =  5939.32973 (m/s)
 
  Axis   Young Modulus        Poisson Ratios
         (GPa)
   X      192.46266       Exy=  0.4770 Exz=  0.1653
   Y      192.46266       Eyx=  0.4770 Eyz=  0.1653
   Z      393.84553       Ezx=  0.3383 Ezy=  0.3383

The elastic Debye temperature evaluation uses the recipe by Anderson (1963), where the averaged sound velocity is evaluated numerically as an integral over all propagation directions. The Debye temperature is proportional to the averaged sound velocity, v_m:

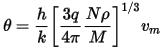
Where:

h is the Planck constant
k is the Boltzmann constant
N is Avogadro's number
ρ is the density
M is the molecular weight of the solid
q is the number of atoms in the molecule.

Elastic Debye temperature and averaged sound velocity are not reported if the calculated elastic constants do not produce physically meaningful sound velocities in some directions (for example, if certain C_ij values or their combinations are negative when they should be positive). This can happen for low quality calculations or for calculations that were not preceded by a geometry optimization (including optimization of the lattice parameters).

The last section of the file contains average properties that describe the elastic response of a polycrystal, for example:

      ====================================================
      Elastic constants for polycrystalline material (GPa)
      ====================================================
                                      Voigt       Reuss        Hill 
Bulk modulus                   :     230.06015   220.35108   225.20562 
Shear modulus (Lame Mu)        :     137.27031   116.19120   126.73075 
Lame lambda                    :     138.54661   142.89028   140.71845 
Young modulus                  :     343.49337   296.46492   320.14092 
Poisson ratio                  :       0.25116     0.27576     0.26308 
Hardness (Tian 2012)           :      16.68027    12.87984    14.74764 
Fracture toughness  (MPa m^0.5):       2.62165     2.36054     2.49228 
 
Universal anisotropy index:       0.95115

This output contains the bulk modulus, shear modulus, Young modulus, and Poisson ratio averaged according to Voigt, Reuss, and Hill schemes (Nye 1957).

In addition, a universal anisotropy index suggested by Ranganathan and Ostoja-Starzewski (2008) is evaluated.

The Vickers hardness in GPa evaluation uses Tian's (2012) empirical formula. This expresses hardness in terms of the polycrystalline bulk, B, and shear, G, moduli (using Pugh's modulus ratio, k=G/B):

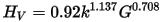
The correlation between the results from this macroscopic model and experimentally measured hardness values is quite good when hardness is larger than 5 GPa. However, the empirical formula overestimates the hardness of softer materials.

Niu et al. (2019) introduced a similar empirical model to estimate fracture toughness, K_IC, from the polycrystalline moduli:

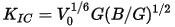
The empirical expressions for Vickers hardness and for fracture toughness cannot be applied if the calculated shear modulus is negative. This can happen when the calculation settings are not sufficiently accurate. In such a case, the summary report does not include the hardness or the fracture toughness.

Calculating elastic constants

Description of the elastic constants file

See Also: