Real-space representations of pseudopotentials

The nonlocality of the pseudopotential only extends over the region occupied by the core of the atom. As the core region is relatively small, it should be possible to deal efficiently with the nonlocality of the pseudopotential by working in real space. Only a small number of operations should be required to project the angular momentum components of each wavefunction in the core of each atom. Furthermore, the number of operations needed to project the angular momentum components of a single wavefunction around a single atom in real space is independent of the size of the system, leading to better scaling with system size than in the reciprocal space projection scheme. The computational cost of the real-space implementation increases with the square of the number of atoms, compared with the cubic relationship that exists for reciprocal space projection methods (Payne et al., 1992).

CASTEP uses the scheme developed originally for norm-conserving potentials (King-Smith et al., 1991) and subsequently generalized for the case of ultrasoft pseudopotentials.

The reciprocal-to-real space transformation involves the following steps:

Select the plane wave cutoff, G_max, which is to be used in the solid-state calculation.
Set χ_l(q) = V_l(q) for 0 < q < G_max and χ_l(q) = 0 for q > γ, where γ is the difference between the ideal Fourier grid size with no wrap-around errors for potential evaluation (at least 4G_max). The Fourier transform of the pseudopotential V_l(q), is defined as:

Eq. CASTEP 22

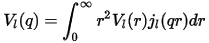
where V_l(r) is the original nonlocal projector and j_l(qr) is the spherical Bessel function.
Select a real-space cutoff radius, R₀. Generally this is about 1.5-2.0 × R_c, where R_c is the core radius used in pseudopotential generation.
Variationally select χ_l(q) in the intermediate region, G_max < q < γ by minimizing:

Eq. CASTEP 23

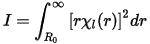
The object of this step is to achieve the best possible convergence of the modified potential in real space.
Transform χ_l(q) back to real space to get χ_l(r ) which is now used in the real-space evaluation of nonlocal potential matrix elements in solid-state calculations.

The modified real-space projectors are no longer identically zero outside R_c, although the minimization in Eq. CASTEP 23 ensures the best possible convergence compatible with the removal of the wrap around error. A quantitative measure of the error introduced by the transformation is given by:

Eq. CASTEP 24

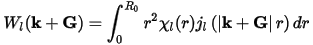
This error function should be small (less than 0.001) for all wavevectors, q, and can be inspected in the CASTEP output file.

One should bear in mind that the use of real-space scheme represents an approximation and that more accurate results are obtained with the reciprocal-space version. The accuracy of the real-space transformation is controlled by the value of the cutoff radius, R₀. The default set of these values in CASTEP is designed to be for accuracy rather than performance. It is advisable to carry out independent tests on small systems before embarking on large-scale calculations with drastically reduced R₀ values.

The real space transformation of the pseudopotential depends on the cutoff energy for plane wave basis set, and thus it is not possible to precalculate real-space projectors in the same way as the reciprocal space potentials (which are provided in CASTEP database).