Ultrasoft pseudopotentials

Ultrasoft pseudopotentials (USP) were introduced by Vanderbilt (1990) in order to allow calculations to be performed with the lowest possible cutoff energy for the plane-wave basis set. Since it is understood that there are inherent limits on optimizing the convergence of norm-conserving pseudopotentials, a completely different approach has been designed.

The rationale behind USP is that, in most cases, a high cutoff energy is only required for the plane-wave basis set when there are tightly bound orbitals that have a substantial fraction of their weight inside the core region of the atom. In these situations, the only way to reduce the basis set is to violate the norm-conservation condition by removing the charge associated with these orbitals from the core region. The pseudo wavefunctions are thus allowed to be as soft as possible within the core, yielding a dramatic reduction in the cutoff energy.

Technically, this is accomplished by introducing a generalized orthonormality condition. In order to recover the full electronic charge, the electron density given by the square moduli of the wavefunctions is augmented in the core regions. The electron density can thus be subdivided into a soft part extending through the unit cell and a hard part localized in the core regions.

USP formalism in solid state

The total energy in the USP scheme has the same form as other pseudopotential plane-wave methods, with the nonlocal potential V_NL given as:

Eq. CASTEP 7

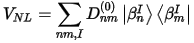
where the projectors β and coefficients D⁽⁰⁾ characterize the pseudopotential and differ for different atomic species. The index I refers to an atomic site. The electron density in the expression for the total energy is given by:

Eq. CASTEP 8

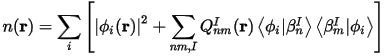
where ϕ are the wavefunctions and Q(r) are the augmentation functions that are strictly localized in the core regions. The ultrasoft potential is fully determined by the local part, V_loc^ion(r) and by the coefficients D⁽⁰⁾, Q, and β. The algorithm that generates these quantities is described below.

The relaxation of the norm-conserving constraint is achieved by introducing a generalized orthonormality condition:

Eq. CASTEP 9

where S is a Hermitian overlap operator:

Eq. CASTEP 10

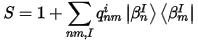
where coefficients q are obtained by integrating Q(r). Kohn-Sham equations can be rewritten for the USP case as:

Eq. CASTEP 11

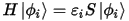
where H can be presented as a sum of kinetic energy and local potential:

Eq. CASTEP 12

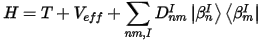
where V_eff contains V_loc^ion(r), Hartree and exchange-correlation terms. All the terms arising from the augmented part of the electron density are grouped with the nonlocal part of the pseudopotential (Eq. CASTEP 7) by defining new coefficients:

Eq. CASTEP 13

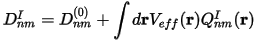
The difference compared with the norm-conserving case is the presence of the overlap operator S, the wave-function dependence of the coefficients D and the fact that the number of projector function β is typically twice as large. A number of calculations related to augmentation charges can be carried out in real space because of the localized nature of the function involved, so that the overall impact of these extra steps on efficiency is not large.

Further technical details of the USP implementation, including expressions for the derivatives of the total energy, can be found in Laasonen et al. (1993).

Pseudopotential generation

As in the norm-conserving case, an all-electron calculation is carried out on a free atom, leading to a screened atomic potential, V_AE(r). For each angular momentum a set of reference energies, ε_l, is chosen. Typically two reference energies are sufficient. These energies should cover the range over which good scattering properties are required. At each reference energy the solution of the radial Kohn-Sham equation which is regular at the origin is obtained. Next cutoff radii R_cl are chosen and for each all-electron wavefunction ψ generated above, a pseudo wavefunction ϕ is constructed. The only constraint is that it should join smoothly to ψ at R_cl. A smooth local potential, V_loc(r), is generated to match V_AE(r) smoothly at a cutoff radius, R_loc. An auxiliary radius, R, is defined to be slightly higher than all of the core radii. Finally, the local orbitals are formed (they vanish beyond R):

Eq. CASTEP 14

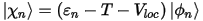
and their matrix of inner products:

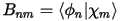
It is now possible to define the quantities needed for the solid state calculation (V_loc^ion(r), D⁽⁰⁾, Q, and β):

Eq. CASTEP 15

Eq. CASTEP 16

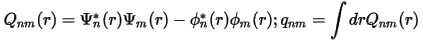
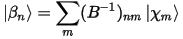
and V_loc^ion(r), D⁽⁰⁾ are produced using a descreening procedure:

Eq. CASTEP 17

Eq. CASTEP 18

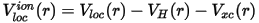
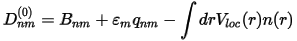
The non-linear core correction term can be introduced in the descreening procedure, Eq. CASTEP 17, in exactly the same way as in the norm-conserving case.

The formalism described above is based on the non-relativistic Schroedinger approach. With CASTEP you can also use a scalar-relativistic approach either as a Koelling-Harmon (1977) scheme or as its approximation commonly referred to as ZORA, zeroth order regular approximation (Lenthe et al. 1994).

The following conditions are satisfied in this scheme:

The pseudo eigenvalues are equal to the all-electron ones, and the corresponding orbitals match exactly outside the core radii.
The scattering properties are correct at each reference energy. Thus, the transferability can be systematically improved by increasing the number of such energies.
The valence charge density is precisely equal to the all-electron valence density in the reference configuration.