Phonons
The basic theory of phonons, or lattice vibrations, in crystals is well understood and has been described in detail in text books such as those by Born and Huang (1954) and Ashcroft and Mermin (1976). The importance of the phonon interpretation of lattice dynamics is illustrated by the large number of physical properties that can be understood in terms of phonons: infrared, Raman, and neutron scattering spectra; specific heat, thermal expansion, and heat conduction; electron-phonon interactions and, thus, resistivity and superconductivity, and so on.
A number of approximations are made in order to arrive at the phonon description of lattice vibrations. First of all, it is assumed that the mean equilibrium position of each ion, i, is a Bravais lattice site, Ri. Secondly, it is assumed that the amplitude of atomic displacements is small compared to interatomic distances. This leads to a harmonic approximation which is sufficiently accurate to describe most of the lattice dynamical effect of interest. However, further refinement, in the form of anharmonic theory, is required to explain physical properties at elevated temperatures when the harmonic approximation breaks down.
The N-ion harmonic crystal can be considered as 3N independent harmonic oscillators, whose frequencies are those of 3N classical normal modes. Thus, at each wave vector, q, in the Brillouin zone there are 3N vibrational modes. There are two equivalent descriptions of this system, either in terms of normal modes or phonons. Phonons are the quanta of the ionic displacement field that describe classical sound; they are similar to photons, the quanta of the radiation field that describe classical light.
The properties of phonons can be described using a harmonic approximation based on the knowledge of just one fundamental quantity, the force constants matrix:
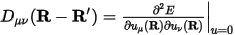
Here u refers to the displacement of a given atom and E is the total energy in the harmonic approximation. This force constants matrix (or Hessian matrix) can also be represented in reciprocal space and the result is commonly referred to as the dynamical matrix:
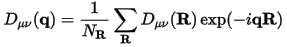
Classical equations of motion can be written in the language of dynamical matrices, as an eigenvalue problem. Each atomic displacement is described in the form of plane waves:
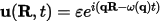
where the polarization vector of each mode, ε, is an eigenvector with the dimension of 3N of the eigenvalue problem:
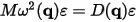
The dependence of the frequency, ω, on the wave vector is known as the phonon dispersion.
Each lattice always has three acoustic modes. Their dispersion relation at small values (near the Γ point) is linear, which is characteristic of sound waves. The rest of the vibrational modes, 3N - 3, in a Bravais lattice with basis are known as optical modes because the long wavelength optical modes in ionic crystals can interact with electromagnetic radiation and are therefore responsible for much of the characteristic optical behavior of such crystals. The frequencies of optical modes are finite at q = 0. A simplistic characterization of acoustic and optical branches (Ashcroft and Mermin, 1976) would be: All ions in a primitive cell move essentially in phase in an acoustic mode and the dynamics is determined by the interaction between cells; an optical mode is one in which the ions within each cell exhibit a molecular vibration mode which is broadened into a band of frequencies due to intercellular interactions.
A popular way of classifying lattice vibrations is based on the relationship between the orientation of the polarization vector, ε, and the propagation direction, q. In an isotropic medium for the case of a monatomic primitive cell it is always possible to choose three solutions for a given q so that one branch (longitudinal) is polarized along the propagation direction and the other two branches (transverse) are polarized perpendicular to this direction. This simple relationship does not hold for an arbitrary q-vector in an anisotropic crystal, nor for a Bravais lattice with basis. It is still common to classify vibrational modes along high symmetry directions in simple lattices based on the transverse and longitudinal description.
Long wavelength vibrations in polar materials deserve a special mention. The long range character of the Coulomb forces gives rise to macroscopic electric fields for longitudinal optic (LO) phonons at the Γ-point in polar semiconductors and insulators. The coupling between longitudinal phonons and the nonperiodic electric field gives rise to LO-TO splitting at the Γ-point. The value of the splitting is determined by the static dielectric constant of the crystal and by the Born effective charge of the ions. The Born effective charge tensor of the sth ion is the partial derivative of the macroscopic polarization with respect to a periodic displacement of all the periodic images of that ion at zero macroscopic electric field. A good review of the practical methods of dealing with this effect is given by Baroni et al., (2001).
Thermodynamic properties of crystals can be evaluated in a fairly straightforward way based on a knowledge of the phonon frequencies across the Brillouin zone (see Ashcroft and Mermin, 1976; Baroni et al., 2001). These quasiharmonic results are quite accurate at moderate temperatures and only small corrections to calculated phase transition properties can be found at temperatures as high as 1000-2000 K (Kern et al., 1999).
Practical schemes for phonon calculations
A good review of the existing schemes can be found in Baroni et al., (2001). The theoretical study of phonon properties has to rely on one of the three available methods for determining the force constants matrix: analytical calculations, supercell calculations, or linear response calculations. The analytical approach is only viable when the energy model is sufficiently simple to allow a direct evaluation of the second derivatives of the energy with respect to atomic displacements (for example, empirical pair potential models). Therefore, it is unsuitable for first principles calculations. Further alternatives such as extracting vibrational properties from molecular dynamics runs (Arias et al., 1992) are less transparent and noticeably more computationally expensive.
The supercell method involves perturbing the positions of the atoms slightly and calculating the reaction forces (Ackland et al., 1997). It is necessary to use supercells of the original cell when interatomic interaction in the system is long ranged. The main advantage of this method (and of the closely related frozen phonon technique) is that there is no need for a new formalism; any total energy scheme like CASTEP can be used to evaluate the forces at a number of carefully selected distorted configurations. The original frozen phonon scheme requires a displacement with the given wave vector and has been successfully used since the early 1980s (Yin and Cohen, 1982; Ho et al., 1984). The force constants matrix evaluation in this formalism has been used to calculate interplanar force constants (Wei and Chou, 1994) and, thus, phonon dispersion along high symmetry directions. More recent applications are based on the full reconstruction of the force constants matrix (Ackland et al., 1997; Parlinski et al., 1997; and references in Baroni et al., 2001).
Linear response calculations seek to evaluate the dynamical matrix directly for a set of q-vectors. The starting point of the linear response approach is evaluation of the second-order change in the total energy induced by atomic displacements. The main advantage of the scheme is that there is no need to artificially increase the cell size in order to accommodate small values of the q-vectors, as in the frozen phonon method, or to overcome the long range interaction problem (force constants matrix from supercell calculations). A more detailed description of the linear response method can be found in Baroni et al., (2001). The CASTEP implementation is described in the Linear response topic.
Interpolation schemes
The force constant matrix (Eq. CASTEP 58) for non-polar insulators and most metals decays proportionally to r-5 or even faster. This fact allows the introduction of an effective interpolation scheme to accelerate phonon calculations within both the finite displacement and linear response formalisms through the introduction of a cutoff radius, Rc, beyond which all the elements of the force constant matrix can be treated as zero. If an approximation for the force constant is available, the dynamical matrix for any given reciprocal vector can be calculated using Eq. CASTEP 59.
Finite displacement: supercell method
In the supercell method, finite displacement calculations are carried out in the supercell, circumventing the sphere described by the cutoff radius, which directly give all the non-zero elements of the force constant matrix.
Linear response: Fourier interpolation
In the Fourier interpolation method, calculations are performed on the regular reciprocal mesh (with a spacing corresponding to the real space cutoff radius). The set of dynamical matrices obtained in these calculations can be used to construct the force constant matrix using Fourier transformation.
Symmetry analysis of vibrations
Symmetry considerations in vibrational analysis are useful for various reasons. For example, the use of symmetry in the CASTEP implementation reduces computational time and the automatic assignment of spectroscopic labels allows you to interpret experimentally measured modes at Γ-points with greater confidence. Symmetry analysis and the subsequent enforcing of symmetry is carried out along the lines suggested by Warren and Worlton (1974). The nomenclature suggested by these authors for labeling symmetry elements is adopted in the CASTEP output. The notation for irreducible representation labels that are common in spectroscopic analysis is specified by IUPAC recommendations (1997).
See Also:
Theory in CASTEP
Phonon density of states
Density of states and partial density of states
Linear response
Thermodynamic calculations